Просто теорема - это то, для чего есть доказательство.
Хм, то есть теорему Ферма до 1995 года называли гипотезой Ферма или проблемой Ферма?
В обсуждении
на math.se есть подборка гипотез, к которым наименьший контрпример большой. Например

и

взаимно просты при
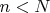
и не взаимно просты при

, где

.
О, это кстати тоже интересно, про очень большие контрпримеры, но это немного другой вопрос.
Я кажется фигово объяснил что хотел. Представим параллельную вселенную. В этой параллельной вселенной есть Ферма (раз уж вспомнил про него), который делает свое знаменитое утверждение. Все тщетно бьются над доказательством или опровержением. Наступает середина ХХ века. Ищем контрпример на компьютере. Очень большие

, но ничего не получается. И вот наступает 1995, появляется параллельный Эндрю Уайлс, который каким-то там образом показывает, что такой контрпример должен существовать. Вот. Я хочу узнать были ли похожие истории в нашем мире.
-- 13.10.2019, 18:38 --В обсуждении
на math.se есть подборка гипотез, к которым наименьший контрпример большой.
Хотя не, это было бы прям то, что мне нужно, если бы там не находили контрпример, а доказывали, что он должен быть. Может я в этом месте туплю? Показать, что контрпример есть

найти этот контрпример? Ну как бы да, но всегда ли?