Если многочлены рассматривать как функции (что является, видимо, самой распространенной интерпретацией)
В алгебре как раз нет. Многочлен - это набор его коэффициентов. А функция - это результат
подстановки числа в многочлен (evaluation map). Причём подставлять можно не только числа:
- если подставить матрицу (в многочлен от одной переменной), то получится многочлен от матрицы;
- если подставить независимую переменную (формальный символ

или

с которым ничего нельзя делать), то получится сам многочлен в символьном виде.
Если многочлены рассматриваются над

или над

то соответствующие функции совпадают тогда и только тогда, когда многочлены совпадают. Но во многих случаях это не так, и многочлены намного богаче, чем соответствующие функции.
Например, рассмотрим

- поле из двух элементов

Всех функций
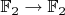
четыре штуки:

Однако многочленов намного больше. Например, есть многочлен

ценный тем, что он неприводим. (А

) Но если бы мы его рассматривали как функцию, то он был бы тождественной 1, конечно же. Ну и конечно, там дальше есть многочлены любой степени, сколь угодно сложные, а функций всё равно всё те же четыре штуки.
-- 12.10.2019 12:58:53 --В любом случае, термин "нулевой" для того, что хочет ТС (ему надо над кольцом вычетов) --- не очень-то хороший.
Термин "нулевой идеал" - это в точности

Так что он не просто нехороший, он не совпадает с тем, что нужно.