Добрый день.
Пытаюсь решить следующую задачу.
В геометрическом пространстве

задана прямоугольная декартова система координат {O;

,

,

}. Необходимо построить матрицу оператора ортогонального отражения

в базисе

,

,

относительно прямой
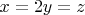
Мои рассуждения такие:
Чтобы построить матрицу оператора нужно определить закон, по которому оператор преобразует векторы пространства. Т.к любой вектор пространства линейно выражается через базисные векторы, то, зная закон, достаточно применить его к базисным векторам и получить искомую матрицу. Каждый вектор пространства может быть разложен в прямую сумму векторов подпространства и его ортогонального дополнения. Таким образом

, где

. Так как ортонональная проекции вектора и его ортогонального отражения совпадают, то отраженный вектор можно искать по формуле

. После того, как я вычислил для произвольного вектора

с координатами

его отражение

с координатами

, я применил этот закон к базисным векторам
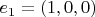
,

,
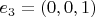
. Однако мой ответ не совпадает с ответом в задачнике. Подскажите, пожалуйста, где я ошибаюсь.