Вернёмся к бутылке Клейна из цилиндров.
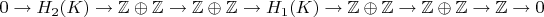
Вроде со вторыми что-то получилось.
Третья стрелка: переводит элемент (1,0) в (1,-1), а элемент (0,1) в (1,1).
Гомоморфизм можно задать матрицей

Она невырождена, следовательно это инъекция. И вторые гомологии нулевые. Это верные рассуждения?
-- 04.10.2019, 12:33 --А что делать с первыми? Нам нужен образ третьей стрелки, но нулевое ядро не означает в данном случае изоморфизм, так ведь?
Например, умножение целых чисел на 2 имеет нулевое ядро, но образ - не все целые числа.
Смотрим.

и

базис в

. Получается, что наш гомоморфизм переводит базис в базис, значит, это изоморфизм. Верно?
Получается, что ядро четвёртой стрелки (это образ третьей) -

, и гомоморфизм четвёртой стрелки нулевой?