Получается мне нужно придумать резольвенту модуля

, когомологии которой я знаю (умею считать)?
У резольвенты, по определению, когомологии должны быть нулевые.
Пусть

модуль над кольцом

. Его резольвента (точнее, левая резольвента) -- это, по определению,
точный комплекс

-модулей

. Но нужна не какая попало резольвента, а, например, проективная.
Вообще на когомологии групп есть 2 точки зрения.
- Точка зрения алгебраиста:
![$H^i(G,\mathbb Z)=\mathrm{Ext}^i_{\mathbb Z[G]}(\mathbb Z,\mathbb Z)$ $H^i(G,\mathbb Z)=\mathrm{Ext}^i_{\mathbb Z[G]}(\mathbb Z,\mathbb Z)$](https://dxdy-02.korotkov.co.uk/f/1/4/5/1455e85e5ba1833bf97c0f2d743f904282.png) .
.
Объяснение. Мы будем иметь дело с модулями над кольцом, которое называется групповою алгеброю группы

и обозначается
![$\mathbb Z[G]$ $\mathbb Z[G]$](https://dxdy-03.korotkov.co.uk/f/e/2/d/e2d2da428f378f22768f705132a274fc82.png)
. Задать на абелевой группе

структуру (для определённости левого)
![$\mathbb Z[G]$ $\mathbb Z[G]$](https://dxdy-03.korotkov.co.uk/f/e/2/d/e2d2da428f378f22768f705132a274fc82.png)
-модуля -- это то же самое, что задать на ней левое действие группы

(автоморфизмами этой абелевой группы). На любой абелевой группе можно задать тривиальное действие: все элементы группы действуют тождественным отображением. Знаком

мы будем обозначать группу целых чисел с таким тривиальным действием
![$\mathbb Z[G]$ $\mathbb Z[G]$](https://dxdy-03.korotkov.co.uk/f/e/2/d/e2d2da428f378f22768f705132a274fc82.png)
. Иными словами, элемент
![$a_1g_1+...+a_ng_n\in\mathbb Z[G]$ $a_1g_1+...+a_ng_n\in\mathbb Z[G]$](https://dxdy-04.korotkov.co.uk/f/f/5/4/f541cb213a2b4bb6e96325b033c467a582.png)
(где

элементы группы,

целые числа) будет действовать на

умножением на

(так как, повторим, все элементы группы действуют тождественным отображением).
Есть функтор
![$\mathrm{Hom}_{\mathbb Z[G]}(\cdot,\mathbb Z)$ $\mathrm{Hom}_{\mathbb Z[G]}(\cdot,\mathbb Z)$](https://dxdy-01.korotkov.co.uk/f/4/8/6/48602ae56654f13b8a02f2d81e836f8982.png)
из категории
![$\mathbb Z[G]$ $\mathbb Z[G]$](https://dxdy-03.korotkov.co.uk/f/e/2/d/e2d2da428f378f22768f705132a274fc82.png)
-модулей в неё же, который переводит

в
![$\mathrm{Hom}_{\mathbb Z[G]}(M,\mathbb Z)$ $\mathrm{Hom}_{\mathbb Z[G]}(M,\mathbb Z)$](https://dxdy-02.korotkov.co.uk/f/9/7/0/97077b72882c81d1ba6cb7e1a1fde25382.png)
. Он точен слева.
![$\mathrm{Ext}^i_{\mathbb Z[G]}(\cdot, \mathbb Z)$ $\mathrm{Ext}^i_{\mathbb Z[G]}(\cdot, \mathbb Z)$](https://dxdy-04.korotkov.co.uk/f/f/7/7/f7752861d3c700d9033e9bbd9f6c618a82.png)
-- это его

-й правый производный функтор.
Пусть вообще есть какой-то точный слева, скажем, контравариантный функтор

: как считать его правые производные

? В гомологической алгебре доказывается, что можно считать следующим образом:
1) выбрать левую резольвенту

, такую что все
 проективны
проективны;
2) выкинуть

и получить комплекс

; обратите внимание, что он квазиизоморфен комплексу
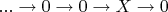
, это очень важно ("квазиизоморфен" значит "имеет такие же когомологии, более того, изоморфизм когомологий индуцируется некоторым цепным отображением");
3) применить к нему

и получить комплекс

4)

-- это

-е когомологии этого комплекса (то есть происходящие из члена с

).
Таким образом, вам нужна
проективная (а не какая попало) резольвента
![$\mathbb Z[G]$ $\mathbb Z[G]$](https://dxdy-03.korotkov.co.uk/f/e/2/d/e2d2da428f378f22768f705132a274fc82.png)
-модуля

. В частности, пойдёт свободная (любой свободный модуль проективен). То, что у вас написано в 1-м посте, происходит из так называемой
стандартной резольвенты модуля

(её ещё называют
бар-резольвентой).
iou подсказывает, что в вашем конкретном случае можно придумать гораздо более простую свободную резольвенту.
-- 28.09.2019, 02:01 --- Точка зрения тополога:
 . Исторически это определение предшествовало предыдущему.
. Исторически это определение предшествовало предыдущему.
Объяснение.

-- это какое-нибудь линейно связное топологическое пространство, у которого фундаментальная группа

, а остальные гомотопические группы нулевые.

довольно редко бывает просто устроено, однако есть стандартная конструкция, которая строит его для любой конечной группы

; подробности смотрите в книге Хатчера "Алгебраическая топология", дополнение к 1-й главе (только там оно обозначается не

, а

). Идея такая: из теории накрытий известно, что если имеется накрытие

с односвязным

, то

действует на

, и фактор по этому действию есть как раз

; более того,

при

. Поэтому достаточно придумать стягиваемое пространство, на котором

действует таким образом, что проекция
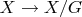
есть накрытие. Его не очень сложно придумать: надо взять симплициальный комплекс, вершины которого занумерованы элементами

, и пусть

действует умножением. Из этой конструкции получается та самая формула, которая у вас в 1-м посте (и которая с точки зрения алгебраиста получена из стандартной резольвенты)!
Однако в вашем конкретном случае, как я уже говорил, не обязательно прибегать к этой конструкции: можно проще (это один из немногих случаев, когда

есть что-то вообразимое). Действительно, в качестве

можно взять бесконечномерное вещественное проективное пространство

: оно накрывается бесконечномерною сферою

(точно так же как

накрывается

для конечного

), а у бесконечномерной сферы все гомотопические группы нулевые. Что же касается

, то у него очень простая клеточная структура: в каждой размерности по одной клетке, причём

-мерная клетка приклеивается посредством отображения

, которое отождествляет диаметрально противоположные точки. Поэтому клеточный цепной комплекс будет

(умножение на 2 или на 0 в зависимости от того, сохраняет ли отражение сферы относительно центра ориентацию или обращает), соответственно коцепной

.
Я надеюсь, это всё не очень страшно выглядит. Если страшно, то не бойтесь, оно не так ужасно, как кажется.