Несколько задач по дискретной теории вероятностей.

[Sdy]

Yadryara в сообщении #1413023 писал(а):

Поскольку посева нет, все соперники в $1$-м раунде равновероятны по условию.

Только сейчас дошло, что под этим подразумевается.
Для команды $8$ в первом туре равновозможен любой противник, то есть любой противник ей попадается с вероятностью $1/7$.
Со 2м раундом пока проблема.

[Yadryara]

Sdy в сообщении #1414295 писал(а):

Со 2м раундом пока проблема.

Какая?

[Sdy]

Yadryara, спасибо за ответ.
Изначально мой подход базировался на $28$ парах. Я только недавно понял, что он в корне неверен, так как выбирать из этих пар "по-простому" нельзя, так как любая взятая пара вида $(a,b)$ делает недействительными любые пары из этих $28$, куда входит $a \vee b$.
Тогда для первого тура я Вашу подсказку понял - действительно любая команда ей попадется с равной вероятностью.
Для второго тура мне бы хотелось сказать, что команде $8$ (которая туда точно прошла) может равновероятно попасться любая команда, кроме той что она выбила и тогда вероятность, что это будет команда $7$ равна $\frac{1}{6}$.
Но данный подход мне кажется неверным это раз.
Два - он не наглядный (для меня). А наглядный пока придумать не получается.

[Yadryara]

Sdy в сообщении #1415218 писал(а):

Тогда для первого тура я Вашу подсказку понял - действительно любая команда ей попадется с равной вероятностью.

Да, по условию. Так называемые равновозможные исходы.

Sdy в сообщении #1415218 писал(а):

Для второго тура мне бы хотелось сказать, что команде $8$ (которая туда точно прошла) может равновероятно попасться любая команда, кроме той что она выбила и тогда вероятность, что это будет команда $7$ равна $\frac{1}{6}$.

Это с какой же радости? А сколько всего команд прошло во $2$-й тур? А с какой вероятностью туда прошла $7$-я команда?

[Sdy]

Yadryara, спасибо за ответ.

Yadryara в сообщении #1415222 писал(а):

А сколько всего команд прошло во $2$-й тур?

Всего во $2$ тур прошло $4$ команды.

Yadryara в сообщении #1415222 писал(а):

А с какой вероятностью туда прошла $7$-я команда?

Она прошла во второй тур с вероятностью $\frac{6}{7}$.
Значит седьмая команда выбыла во втором туре с вероятностью $\frac{1}{4}\frac{6}{7}$
Команда $7$ выбыла либо в первом туре, либо во втором.
В первом туре она выбывает с вероятностью $\frac{1}{7}$. Во втором туре - с вероятностью написанной выше.
Значит вероятность того что $7$ команда выбыла до финала равна $\frac{5}{14}$.
А вероятность того что команда $7$ встретится в финале с командой $8$ равна $\frac{9}{14}$.

[Yadryara]

Sdy в сообщении #1415267 писал(а):

Она прошла во второй тур с вероятностью $\frac{6}{7}$.

Да.

Sdy в сообщении #1415267 писал(а):

Значит седьмая команда выбыла во втором туре с вероятностью $\frac{1}{4}\frac{6}{7}$

Неа. Чуток внимательнее надо бы.

[Sdy]

Yadryara, спасибо за ответ.
Да, $\frac{1}{3}$ конечно. И всё те же рассуждения.

-- 15.09.2019, 19:58 --

Осталось мне задать вероятностное пространство для данной задачи, которое я тоже хочу выложить на проверку, так как с ним пока не задаётся. Ну, точнее явно задать пространством элементарных исходов, остальные элементы будут и так понятны.

[Sdy]

Хотел бы всё-таки понять, могу ли я рассуждать так:
Рассуждение.
Наше пространство элементарных исходов на первом этапе - всевозможные четверки из пар, где в каждой паре есть только одна из команд и внутри четверки никакая команда не повторяется дважды.
Тогда в такую четверку первую команду берём $28$ способами, вторую $15$, третью $6$, четвертая влетает однозначно. При этом две четверки считаются одинаковыми, если в них одинаковые пары команд, то есть порядок выбора роли не имеет.
Тогда пространство исходов состоит из $\frac{28\cdot15\cdot6}{4!}$ исходов.
Благоприятное событие состоит из $\frac{15\cdot6}{3!}$ исходов. То есть точно взяли пару $\{7, 8\}$, а для остальных нужно убить порядок.
Значит вероятность, что $8$ встретится с $7$ в первом туре равна $\frac{1}{7}$

Очень уж хочется разобраться с моим рассуждением, с которого я и пытался начинать решение.

-- 17.09.2019, 04:37 --

Рассуждение для второго тура.
Пусть $7$ прошла во второй тур.
Тогда пространство элементарных исходов состоит из двоек, которые состоят из пар (их всего $6$). Тогда мощность пространства элементарных исходов $\frac{6\cdot5}{2}$.
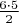
Благоприятных исходов у нас $5$.
Значит $7$ вылетела во втором туре с вероятностью $\frac{1}{3}$.