Я признаю, что виноват в своём хамстве. Это чисто моя вина. Признаю прямо и открыто, без тени подтекста. Буду признателен, если вернёмся к задаче.
Смотрите, что получается: (программный код для Asymptote под спойлером ниже. Набросан наспех кое-как, без оформления, но ошибок нет. Копипаст, Enter, - и картинки создадутся те же самые на любом компьютере в мире.)
При одном источнике:
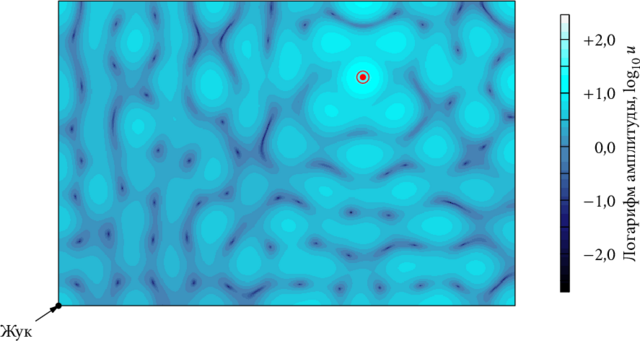
При трёх источниках:

Спойлер с кодом (на всякий случай)
(Оффтоп)
Код:
// Полный бассейн с волнами
settings.tex = "pdflatex";
import unicode;
bool cochineal = true;
if (cochineal) {
texpreamble("
\usepackage{amsmath,amstext,mathrsfs}
%\usepackage[garamond]{mathdesign}
\usepackage{cochineal}
\usepackage[varqu,varl,var0]{inconsolata}
\usepackage[scale=.95,type1]{cabin}
\usepackage[cochineal,bigdelims,vvarbb]{newtxmath}
% Каллиграфия и рукопись
% pxtx - простые и даже брутальные
% euler - тоже простой, но аккуратнее и прямостоящий
% rsfso - с завитушками, тонкий
% boondoxo - с завитушками, но жирнее
\usepackage[cal=pxtx,scr=rsfso]{mathalfa}
\usepackage{dcomma}
");
} else {
texpreamble("
\usepackage{amsmath,amstext,amssymb}
\usepackage[T2A,T1]{fontenc}
\usepackage{dcomma}
\usepackage{mathptmx}
\usepackage{tempora}
");
}
import babel;
babel("russian");
import x11colors;
import markers;
import graph;
import palette;
size(6inches,0);
// Размеры бассейна
real a=3;
real b=2;
// Источники
pair[] src = {(2,1.5),(1.6,1),(2.7,1.1)};
// Функция, возвращающая амплитуду колебаний в запрошенной точке
int kmn = 5; // количество учитываемых отражений
pair gama = (0,4pi);
real amp(real x, real y) {
pair u = (0,0); // накопитель
real dist;
for (pair p : src) {
for (int n=-kmn; n<=kmn; n+=1) {
for (int m=-kmn; m<=kmn; m+=1) {
dist = sqrt((2*m*a+p.x-x)^2+(2*n*b+p.y-y)^2);
u += exp(-gama*dist)/dist;
dist = sqrt((2*m*a-p.x-x)^2+(2*n*b+p.y-y)^2);
u += exp(-gama*dist)/dist;
dist = sqrt((2*m*a-p.x-x)^2+(2*n*b-p.y-y)^2);
u += exp(-gama*dist)/dist;
dist = sqrt((2*m*a+p.x-x)^2+(2*n*b-p.y-y)^2);
u += exp(-gama*dist)/dist;
}
}
}
return log10(abs(u));
}
real amp2(real x, real y) {
return x+y;
}
pen[] pal = Gradient(8, black, MidnightBlue, SteelBlue, Cyan, WhiteSmoke);
int kk = 200; // количество точек
bounds img = image(amp,-(a,b)*0,(a,b),pal,nx=(int)a*kk,ny=(int)b*kk);
picture pic;
palette(pic,"Логарифм амплитуды, $\log_{10} u$",img,(0,0),(2mm,6.5cm),Right,pal,PaletteTicks("$%+#.1f$"));
add(pic.fit(),point(E),30E);
fill(circle((0,0),0.02),black+5pt);
draw((0,0)-- (-0.05*(a,b)),BeginArrow(2mm));
label("Жук", (-0.05*(a,b)),SW);
draw((0,0)--(a,0)--(a,b)--(0,b)--cycle);
for (pair p : src) {
draw(circle(p,0.04),red);
fill(circle(p,0.02),red);
}
//-----------------
shipout(bbox(2pt,nullpen));
Корявое слово "gama" в коде потому, что "gamma" занята гамма-функцией. "gama" - коэффициент распространения. Первое число в скобках - коэффициент затухания, неперы на единицу длины. Второе - волновое число, радианы на единицу длины.
Если кто будет пробовать - число отражений до пары сотен на скорость расчёта не влияет. А вот число точек в картинке сильно замедляет. При 50 точках картинка создается за пару секунд, а при 200 точках (int kk=200) около 3 минут на 2 ГГц процессоре.