Хи-квадрат для распределения Лапласа

[Евгений Машеров]

Andrey_Kireew в сообщении #1414577 писал(а):

AK=AK+(10-100*p)*(10-100*p)/(100*p*(1-p));

Прошу прощения, это случайно попал продукт экспериментов по усовершенствованию, в приведенных выше результатах расчётов в знаменателе везде стояло p.
Ну а о соответствии $\chi^2$ можно судить по моментам. Они для стандартного в точности соответствуют хи-квадрат, а у Вас отличаются, причём это отличие не объяснить тем, что тоже хи-квадрат, но с другим числом степеней свободы.
Что до использования равномерного - это случай, наиболее благоприятный Вашей модели. При неравномерных ячейках должна вырасти дисперсия интерквантильного расстояния.

[Andrey_Kireew]

Евгений Машеров в сообщении #1414571 писал(а):

Проблем вообще не вижу, программа мне представляется проще, чем Ваша (разумеется, это субъективно), раскидывание по ячейкам линейная сложность, тогда как сортировка в лучшем случае $N\ln N$, а то и квадратична, так что и со скоростью не вижу преимуществ. Но, разумеется, вопрос в том, насколько можно верить результатам. Хи-квадрат - можно. А "равносоставленному"?

С этим согласен, в моей программе матлаб больше всего тормозит при подсчёте частот, а не при сортировке, этот участок можно существенно ускорить, и тогда, без сортировки, равноинтервальная получится конечно быстрее. Но я имел в виду совсем не то, а проблему малых частот, которая сильно усложняет алгоритм. Впрочем, об этом я уже писал.

-- 11.09.2019, 20:24 --

Евгений Машеров в сообщении #1414592 писал(а):

Что до использования равномерного - это случай, наиболее благоприятный Вашей модели

да что Вы такое говорите? А мне всегда казалось наоборот, равномерный закон - единственный случай, когда не проявляются главные недостатки равноинтервальной группировки. Именно по этому Вы его и выбрали. С другим законом, будь то нормальный, или тем более лапласов, Ваша программа не сможет продемонстрировать представленных результатов даже близко. И Вы об этом прекрасно знаете, так что не надо ссылаться на стремление создать оптимальные условия для равнонаполненной группировки.

[Евгений Машеров]

Ну, посмотрите распределения квантилей.

[Andrey_Kireew]

Вот, что у меня получилось для для равномерного закона (100000 симуляций):

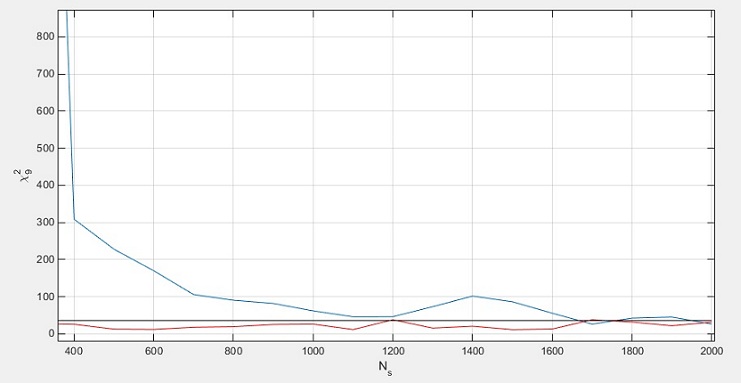
синяя это равнонаполненная, красная - равноинтервальная, чёрная линия - критический уровень 0.01.
В целом, динамика похожа на то что представили Вы.
Скажем так, начиная от 1700, этим можно начинать пользоваться, ну а менее 700, уже совершенно непригодно.

Если всё так как Вы пишите, почему бы не привести аналогичные результаты для нормального распределения, как у меня?

-- 11.09.2019, 22:25 --

Ну а вот, аналогично, с нормальным законом (число симуляций здесь только 10 тыс. поэтому колебания больше):

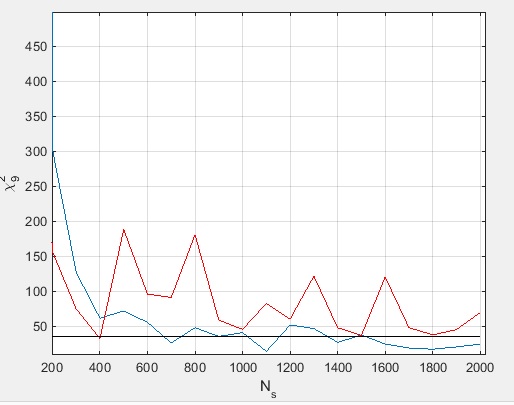
синяя равнонаполненная, красная - равноинтервальная, чёрная - уровень значимости 0.01.

Как видите Евгений Машеров, с нормальным распределением ситуация немного изменилась, вернее сказать поменялась в корне. Хотелось бы особенно отметить, что все равноинтервальные группировки, не удовлетворяющие критерию Кокрена (N>1) были отброшены и не учитывались при оценке распределения статистики, а это примерно 15% всех наблюдений. Иначе не о каком соответствии Хи квадрат не приходится даже и говорить. И даже при этом, равноинтервальная группировка оказывается хуже.
А равнонаполненная, напротив, опровергая Ваше необоснованное утверждение

Евгений Машеров в сообщении #1414592 писал(а):

использования равномерного - это случай, наиболее благоприятный Вашей модели.

оказывается даже лучше, и чем при равномерном распределении, и лучше самой равноинтервальной группировки (впрочем, это полностью соглассуется с ранее представленными мной результатами).

Так, что равномерный закон это очень хорошо, но представляется, что здесь он притянут "уши", исключительно для того, чтобы хоть как то опорочить все неоспоримые достоинства равнонаполненной группировки.

[Andrey_Kireew]

Уважаемые Евгений Машеров, обнаружена ошибка.
При равнонаполненной группировке Вы берёте нижнюю границу крайнего левого интервала равной значению минимального элемента

Left=R(1);

и верхнюю границу, равную значению максимального элемента элемента

Right=R(100);

У меня было так же, но это в корне не верно. В данном случае границы распределения есть его параметры, поэтому, при проверке простой гипотезы необходимо сделать так

Left=0;
........
Right=1;

Я попробовал, после 800 наблюдений оба графика практически сливаются.
Видимо, по этой причине с нормальным распределением получалось лучше.