Независимость собственных векторов

[SemDvs]

Добрый день!
Собственный базис предполагает независимость собственных векторов. Подскажите пожалуйста, откуда следует эта независимость собственных векторов?
Облазиз гугл, но так и не понял :(

[arseniiv]

Ну, мы как раз выбираем их так, чтобы они были независимы и покрывали все собственные подпространства. Мы вполне могли бы взять недостаточно или слишком много собственных векторов. (Разумеется, это про случай, когда такой базис вообще существует.)


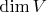
UPD: Вот например возьмём оператор умножения на скаляр $\lambda$: у него одно собственное число $\lambda$ и любой вектор — собственный, соответствующий этому числу, и мы можем выбрать собственный базис весьма разнообразно — вообще любые $\operatorname{dim}V$ независимых векторов. С другой стороны, возьмём оператор, имеющий в некотором базисе матрицу $\operatorname{diag}(\lambda_1,\ldots,\lambda_n)$, где все $\lambda_i$ разные. Этот базис будет одним из собственных для этого оператора, и другие можно будет получить только перестановкой его векторов и умножением их на ненулевые константы — свобода минимальна. Для других операторов, имеющих собственные базисы, случаи промежуточные.

[Brukvalub]

Если бы у каждого линейного оператора был бы базис из собственных векторов, то Жордан не смог бы придумать свою ЖНФ. Вот собственные векторы, отвечающие разным собственным значениям, всегда линейно независимы, такая теорема есть.

[SemDvs]

arseniiv в сообщении #1414057 писал(а):

Ну, мы как раз выбираем их так, чтобы они были независимы и покрывали все собственные подпространства.

Получается, это следует из собственных значений. Тогда вопрос по другому: почему разные собственные значения порождают независимые собственные вектора?

[Xaositect]

Это должно быть в учебнике, см. напр. Кострикин "Введение в алгебру" II часть, 2.3.4, лемма 1.
Доказательство простое по индукции, если есть линейная зависимость, то, применив к обеим частям оператор, можно получить еще одну зависимость и исключить один из векторов.