Хотел бы уточнить. Несмотря на то что до того как я немного залез в математическую логику неоднократно эти правила мною применялись без каких либо вопросов, как только посмотрел на них формально, немного запутался.
1.Корректность доказательства от противного.Пусть имеется утверждение, имеющее вид

. При доказательстве от противного мы предполагаем, что данное утверждение неверно. Но в силу определения импликации утверждение неверно только если

. Тогда мы и предполагаем это. Приходим к противоречию, но тогда импликация должна быть верна.
И вот тут у меня заскок. Импликация верна в трёх случаях
1.
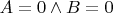
.
2.

.
3.

.
Правильно ли я понимаю, что мы отметаем остальные случае кроме третьего в силу того что при доказательстве утверждения нам обычно дано, что

- верно? Ну, там при таких-то

верно то-то. Или из того что сходится, следует то-то. То есть мы предполагаем, что в условиях теоремы

- верно, и тогда остается только третий вариант?
2.Закон контрапозиции.(Я же правильно понял, что его так и называют используя русский язык? По крайне мере так мне говорит Google. Звучит просто непривычно.)
Необходимо доказать, что

.
Доказательство.1.

. Если

неверно, то

. Но тогда и

неверно. Если же оно верно, тогда возможны три ситуации:
1.1.
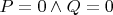
. Но тогда и

верно.
1.2.

.
1.3.
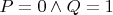
.
В обоих случаях также видно, что в силу определения импликации условие теоремы выполнено.
2.Обратно доказывают точно также.
Таким образом получаю, что закон контрапозиции верен и я могу его использовать в доказательстве утверждений.

.
Тут вопросов не возникло, на случай если я заблуждаюсь (в книге об этом было оговорено кратко) привел полное рассуждение.
-- 09.09.2019, 20:52 --beroal, спасибо за ответ.
Вот таким образом я для себя пока их и определил.
Проще всего сказать, что логические связки — это слова непонятного языка для создания грамматических конструкций, и дать правила вывода, которые позволяют выводить математические утверждения и косвенно задают смысл логических связок.