Кострикин, определитель матрицы специального вида

[Paul Ivanov]

Дана матрица специального вида размера $(n-1) \times (n-1)$, которая выглядит так:

$$\begin{bmatrix} \frac{1}{2!}& \frac{1}{3!} & \frac{1}{4!} & \cdots & \frac{1}{n!}\\ 1 & \frac{1}{2!} & \frac{1}{3!} & \cdots & \frac{1}{(n-1)!}\\ 0 & 1 & \frac{1}{2!} & \cdots & \frac{1}{(n-2)!}\\ \vdots & \vdots & \vdots & & \vdots\\ 0 & 0 & 0 & \cdots & \frac{1}{2!} \end{bmatrix}$$

В задаче требуется доказать, что при чётных $n$ начиная с $4$ определитель такой матрицы равен нулю. Пусть определитель такой матрицы порядка $n-1$ называется $P_n$. Тогда $P_n$ определено для всех $1<n \in \mathbb{N}$ однозначно. Пусть так же $P_1=1$. Отсюда, раскладываем определитель по первой строке и далее получаем, что $P_n=\frac{1}{2!}P_{n-1}-\frac{1}{3!}P_{n-2}+\frac{1}{4!}P_{n-3}-...+(-1)^n \frac{1}{n!}P_1$
Как я далее с этой матрицей не крутился ничего путного не получилось, все стандартно применяемые к специальным матрицам приёмы здесь не срабатывают, тогда я посмотрел, что предлагает Кострикин в качестве идеи для решения и суть я понял так, мы должны подобрать такую функцию f(x), которая раскладывается в ряд тейлора $f(x)=1+b_1 x+ b_2 x^2 +...$, где модули чисел $b_3,b_5,b_7,...$ совпадают с модулями чисел $P_3, P_5, P_7,...$ и тогда останется только показать, что функция $f(x)-1-b_1 x$ 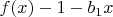является чётной. В частности предлагается воспользоваться тождеством $1=(1+b_1 x+b_2 x^2+...)(1+\frac{x}{2!}+\frac{x^2}{3!}+...)$, где $b_1=-P_1, b_2=P_2, b_3=-P_3$ и т.д. Но даже зная
это тождество я не смог додуматься, как его вывести естественным путём.
Прошу либо помочь прийти естественным образом к этому тождеству, либо предложить идею, как прийти к решению другим путём.

[DeBill]

Paul Ivanov в сообщении #1409626 писал(а):

прийти естественным образом к этому тождеству,

Естественный путь называется "метод производящих функций". Идея метода состоит в следующем:
при работе с последовательностью ($P_n$) полезно рассмотреть функцию $\sum\limits_{n=0}^{\infty} P_n x^n$. (классики грят: вместо того чтобы тащить огромную кучу мелких предметов - (Пэ-энных), давайте сложим их в один большой мешок (функцию Пэ) - тащить станет невпример легче (а в случае надобности, нужный предмет извлекается из мешка дифференцированием и подстановкой нуля...)).
Метод весьма эффективен именно при работе с последовательностями, заданными реккурентно. Только надо уметь чуток работать с рядами (перемножать, дифференцировать, и т.п.). Например, если $\sum\limits_{}^{}a_nx^n \cdot \sum\limits_{}^{}b_nx^n =\sum\limits_{}^{}c_nx^n$, то $c_n=a_0b_n+a_1b_{n-1}+...+a_nb_n$.
Ну, в Вашей задаче: вводим производящую функцию для Вашей последовательности. Домножим Ваше энное уравнение на $x^n$, и сложим их все. Теперь внимательное поглядение на полученное равенство (формулу ту я неспроста написал) дает замечательное равенство...
Кстати, тот множитель, с факториалами: не слабо явно вычислить, что это за функция (правда, она чем то похожа на экспоненту?)

[Paul Ivanov]

Спасибо, идею понял, всё получилось