Здравствуйте, уважаемые участники форума. У меня появилась сложность при решении волноводной задачи с источником. Поскольку сложность задачи математическая, то в физику вопроса я особо вдаваться не буду, хотя она очевидная. Известно, что колебания в волноводе можно описать так называемой системой телеграфных уравнений - это система линейных обыкновенных дифференциальных уравнений первого порядка. При этом вид колебаний может быть любым. В моем случае эта система выглядит следующим образом


где

и
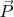
- вектора неизвестных функций,

,

,

- заданные матрицы, которые зависят от z,

и
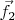
- вектора, связанные с источником колебаний.
Такую систему принято численно считать методом Рунге-Кутта, при этом хорошо известно что при некоторых параметрах решение становится неустойчивым. Такое решение соответствует модам колебаний с частотой ниже частоты отсечки и представляющие собой экспоненциально затухающие колебания. Одним из подходов, который позволяет решить такую проблему, является замена переменных и составление уравнения Риккати для импеданса Z, который связывает U и P соотношением

.
Если продифференциировать это равенство и избавиться от производных, используя систему телеграфных уравнений, то в случае отсутствия источника можно получить такую систему уравнений

или, поскольку

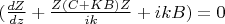
Данное уравнение уже не имеет такой проблемы, решив его, можно уже потом находить вектора исходных неизвестных, причем также без проблем с устойчивостью решения.
Однако, в случае наличия источников ( векторов

и
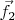
) получить уравнение только для импеданса не получается. Подскажите пожалуйста как решить эту проблему. Возможно сам импеданс нужно определять по другому? Заранее спасибо.