Индексы в скобках

[Roman_T]

Кострикин во Введении в алгебру, т. 1, с. 68 писал(а):

Пример 2. В пространстве $\mathbb{R}^n$ рассмотрим так называемые единичные векторы-строки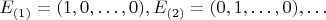
$E_{(1)}=(1,0,\dots,0), E_{(2)}=(0,1,\dots,0),\dots$

Почему индексы в скобках?

там же, далее по тексту, он писал(а):

Единичные векторы-столбцы будем обозначать символами
$E^{(1)}=[1,0,\dots,0], E^{(2)}=[0,1,\dots,0],\dots$

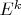
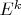
Я предположил что верхний индекс в скобках чтобы не путать $E^{(k)} и $E^k$. Хотя мне непонятно что в данном случае означает $E^k$ (возможно это будет понятно дальше по мере чтения).
А нижний индекс заключен в скобки чтобы было одинаково, верхний в скобках и нижний в скобках.
Правильно ли я понял?

[iifat]

Тут главное — не заморачиваться. Всякий автор имеет право на свои обозначения, лишь бы они были нормально определены.

[Roman_T]

Ясно, спасибо за ответ.

Я еще нашёл что ранее автор пишет что $\mathbb{R}^1$ принято отождествлять с $\mathbb{R}$. Так что можно сказать что $E_{(k)}$ тождественно $E_k$.

[iifat]

Roman_T в сообщении #1411834 писал(а):

Так что можно сказать что $E_{(k)}$ тождественно $E_k$

Не думаю. Полистал немного — автор последовательно обозначает базисные векторы $E_{(i)}$, хотя все прочие — $X_i$. Видимо, где-то в книге $E_i$ обозначено что-то другое (хотя возможно, например, этот кусок в книгу не вошёл; или, например, вошёл в другую). В общем, повторюсь: не заморачивайтесь грамматическим анализом обозначений. Нет в нём никакого сакрального смысла. Это просто обозначения.

[ewert]

Roman_T в сообщении #1411834 писал(а):

Я еще нашёл что ранее автор пишет что $\mathbb{R}^1$ принято отождествлять с $\mathbb{R}$.

Это не принято так -- это просто логично. Дело в том, что $\mathbb{R}^n$ -- это именно степень, это декартово произведение $n$ экземпляров просто $\mathbb{R}$. Ну а первую степень практически никогда не пишут -- разве что тогда, когда хотят подчеркнуть, что она именно первая (а могла бы быть и любой).

[Roman_T]

Понятно, спасибо за разъяснения!