Итак, раз лучше идей не поступило, будем действовать по намеченному пути. (На самом деле, я последний интеграл уже численно взял: машина железная, что ей пару миллиардов арксинусов посчитать; но раз уж тему открыл, надо и закрывать самому). Для начала обезразмерим:

,

,
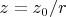
,

и искомый интеграл равен
![$$
\begin{array}{rl}
V(x_0,y_0,z_0,r)=&\displaystyle\frac{r^3}{2}\int\limits_{z}^{\sqrt{1-x^2-y^2}}\left[(1-t^2)\left(\frac{\pi}{2} -\arcsin\frac{y}{\sqrt{1-t^2}}-\arcsin\frac{x}{\sqrt{1-t^2}}\right) +\right.\\
+&\displaystyle\left. 2xy-x\sqrt{1-x^2-t^2}-y\sqrt{1-y^2-t^2}\right]dt
\end{array}$$ $$
\begin{array}{rl}
V(x_0,y_0,z_0,r)=&\displaystyle\frac{r^3}{2}\int\limits_{z}^{\sqrt{1-x^2-y^2}}\left[(1-t^2)\left(\frac{\pi}{2} -\arcsin\frac{y}{\sqrt{1-t^2}}-\arcsin\frac{x}{\sqrt{1-t^2}}\right) +\right.\\
+&\displaystyle\left. 2xy-x\sqrt{1-x^2-t^2}-y\sqrt{1-y^2-t^2}\right]dt
\end{array}$$](https://dxdy-04.korotkov.co.uk/f/3/9/5/39547df96467acc8401bc23ff658829b82.png)
Далее возьмём по частям один из арксинусов:
![$$
\displaystyle-\int\left[(1-t^2)\arcsin\frac{y}{\sqrt{1-t^2}}\right]dt=\displaystyle\left. -\left(t-\frac{t^3}{3}\right)\arcsin\frac{y}{\sqrt{1-t^2}}\right| + \displaystyle\int\frac{t^2(1-t^2/3)}{1-t^2}\frac{y}{\sqrt{1-t^2-y^2}}dt
$$ $$
\displaystyle-\int\left[(1-t^2)\arcsin\frac{y}{\sqrt{1-t^2}}\right]dt=\displaystyle\left. -\left(t-\frac{t^3}{3}\right)\arcsin\frac{y}{\sqrt{1-t^2}}\right| + \displaystyle\int\frac{t^2(1-t^2/3)}{1-t^2}\frac{y}{\sqrt{1-t^2-y^2}}dt
$$](https://dxdy-04.korotkov.co.uk/f/f/c/2/fc2a3bbbcf5886997c04d9577d45108282.png)
Вторая часть берётся с помощью
WolframAlpha и долгого и муторного упрощения того, что оно насчитало в комплексных переменных:
![$$
\begin{array}{rl}
&\displaystyle\int\frac{t^2(1-t^2/3)}{1-t^2}\frac{y}{\sqrt{1-t^2-y^2}}dt=\\
=&\displaystyle-\frac{1}{6}\left[ty\sqrt{1-t^2-y^2}+y(3+y^2)\arctg\frac{t}{\sqrt{1-t^2-y^2}}+2i\ln\frac{\left(\sqrt{1-t^2-y^2}+ity\right)^2}{(1-t^2)(1-y^2)}\right]=\\
=&\displaystyle-\frac{1}{6}\left[ty\sqrt{1-t^2-y^2}+y(3+y^2)\arcsin\frac{t}{\sqrt{1-y^2}}-4\arctg\frac{ty}{\sqrt{1-t^2-y^2}}\right]\\
\end{array}$$ $$
\begin{array}{rl}
&\displaystyle\int\frac{t^2(1-t^2/3)}{1-t^2}\frac{y}{\sqrt{1-t^2-y^2}}dt=\\
=&\displaystyle-\frac{1}{6}\left[ty\sqrt{1-t^2-y^2}+y(3+y^2)\arctg\frac{t}{\sqrt{1-t^2-y^2}}+2i\ln\frac{\left(\sqrt{1-t^2-y^2}+ity\right)^2}{(1-t^2)(1-y^2)}\right]=\\
=&\displaystyle-\frac{1}{6}\left[ty\sqrt{1-t^2-y^2}+y(3+y^2)\arcsin\frac{t}{\sqrt{1-y^2}}-4\arctg\frac{ty}{\sqrt{1-t^2-y^2}}\right]\\
\end{array}$$](https://dxdy-02.korotkov.co.uk/f/d/f/a/dfaf029b61cfbbe4338078201cfe365882.png)
Страшновато, громоздко, но правильно: с численно взятым интегралом совпадает. Из остальных членов остаётся почти табличный интеграл

Замечу, что обе его части немного сократятся с подсчитанными выше:

, а

. Результат взятия интеграла:
![$$
\begin{array}{rl}
&\displaystyle\int\left[(1-t^2)\left(\frac{\pi}{2} -\arcsin\frac{y}{\sqrt{1-t^2}}-\arcsin\frac{x}{\sqrt{1-t^2}}\right) + 2xy-x\sqrt{1-x^2-t^2}-y\sqrt{1-y^2-t^2}\right]dt = \\
=&\displaystyle\left(t-\frac{t^3}{3}\right)\left(\frac{\pi}{2} - \arcsin\frac{y}{\sqrt{1-t^2}}-\arcsin\frac{x}{\sqrt{1-t^2}}\right) - \frac{2ty}{3}\sqrt{1-t^2-y^2}-\frac{y}{3}(3-y^2)\arcsin\frac{t}{\sqrt{1-y^2}}+\\
+&\displaystyle \left.\frac{2}{3}\arctg\frac{ty}{\sqrt{1-t^2-y^2}} - \frac{2tx}{3}\sqrt{1-t^2-x^2}-\frac{x}{3}(3-x^2)\arcsin\frac{t}{\sqrt{1-x^2}}+\frac{2}{3}\arctg\frac{tx}{\sqrt{1-t^2-x^2}}+ 2xyt\right|
\end{array}$$ $$
\begin{array}{rl}
&\displaystyle\int\left[(1-t^2)\left(\frac{\pi}{2} -\arcsin\frac{y}{\sqrt{1-t^2}}-\arcsin\frac{x}{\sqrt{1-t^2}}\right) + 2xy-x\sqrt{1-x^2-t^2}-y\sqrt{1-y^2-t^2}\right]dt = \\
=&\displaystyle\left(t-\frac{t^3}{3}\right)\left(\frac{\pi}{2} - \arcsin\frac{y}{\sqrt{1-t^2}}-\arcsin\frac{x}{\sqrt{1-t^2}}\right) - \frac{2ty}{3}\sqrt{1-t^2-y^2}-\frac{y}{3}(3-y^2)\arcsin\frac{t}{\sqrt{1-y^2}}+\\
+&\displaystyle \left.\frac{2}{3}\arctg\frac{ty}{\sqrt{1-t^2-y^2}} - \frac{2tx}{3}\sqrt{1-t^2-x^2}-\frac{x}{3}(3-x^2)\arcsin\frac{t}{\sqrt{1-x^2}}+\frac{2}{3}\arctg\frac{tx}{\sqrt{1-t^2-x^2}}+ 2xyt\right|
\end{array}$$](https://dxdy-04.korotkov.co.uk/f/3/7/1/371715f4cf24f480fba2e42b3778397e82.png)
Длинно, но не так уж и страшно. Впрочем, чтобы стало страшно, сюда ещё и пределы подставить можно:
![$$
\begin{array}{rl}
V(x_0,y_0,z_0,r)=&\displaystyle\frac{r^3}{6}\left[t\left(3-t^2\right)\left(\frac{\pi}{2} - \arcsin\frac{y}{\sqrt{1-t^2}}-\arcsin\frac{x}{\sqrt{1-t^2}}\right)-\right.\\
&\left. \left.-\displaystyle 2ty\sqrt{1-t^2-y^2} - y(3-y^2)\arcsin\frac{t}{\sqrt{1-y^2}}+2\arctg\frac{ty}{\sqrt{1-t^2-y^2}}-\right.\right.\\
&\left. \left.-\displaystyle 2tx\sqrt{1-t^2-x^2} - x(3-x^2)\arcsin\frac{t}{\sqrt{1-x^2}}+2\arctg\frac{tx}{\sqrt{1-t^2-x^2}}+ 6xyt\right]\right|\limits_{z}^{\sqrt{1-x^2-y^2}}=\\
=&\displaystyle\frac{\sqrt{r^2-x_0^2-y_0^2}}{6}\left(2r^2+x_0^2+y_0^2\right)\left(\frac{\pi}{2} - \arcsin\frac{y_0}{\sqrt{x_0^2+y_0^2}}-\arcsin\frac{x_0}{\sqrt{x_0^2+y_0^2}}\right)-\\
&-\displaystyle\frac{z_0}{6}\left(3r^2-z_0^2\right)\left(\frac{\pi}{2} - \arcsin\frac{y_0}{\sqrt{r^2-z_0^2}}-\arcsin\frac{x_0}{\sqrt{r^2-z_0^2}}\right)-\\
&-\displaystyle\frac{y_0}{6}\left(3r^2-y_0^2\right)\left(\arcsin\frac{\sqrt{r^2-x_0^2-y_0^2}}{\sqrt{r^2-y_0^2}}-\arcsin\frac{z_0}{\sqrt{r^2-y_0^2}}\right) -\\
&-\displaystyle\frac{x_0}{6}\left(3r^2-x_0^2\right)\left(\arcsin\frac{\sqrt{r^2-x_0^2-y_0^2}}{\sqrt{r^2-x_0^2}} -\arcsin\frac{z_0}{\sqrt{r^2-x_0^2}}\right)+\\
&+\displaystyle \frac{r^3}{3}\left(\arctg\frac{y_0\sqrt{r^2-x_0^2-y_0^2}}{rx_0} -\arctg\frac{y_0z_0}{r\sqrt{r^2-y_0^2-z_0^2}}\right)+\\
&+\displaystyle \frac{r^3}{3}\left(\arctg\frac{x_0\sqrt{r^2-x_0^2-y_0^2}}{ry_0}-\arctg\frac{x_0z_0}{r\sqrt{r^2-x_0^2-z_0^2}}\right)+\\
&+\displaystyle \frac{x_0 y_0}{3}\sqrt{r^2-x_0^2-y_0^2}+\frac{z_0 y_0}{3}\sqrt{r^2-z_0^2-y_0^2} + \frac{z_0 x_0}{3}\sqrt{r^2-z_0^2-x_0^2}-x_0y_0z_0
\end{array}$$ $$
\begin{array}{rl}
V(x_0,y_0,z_0,r)=&\displaystyle\frac{r^3}{6}\left[t\left(3-t^2\right)\left(\frac{\pi}{2} - \arcsin\frac{y}{\sqrt{1-t^2}}-\arcsin\frac{x}{\sqrt{1-t^2}}\right)-\right.\\
&\left. \left.-\displaystyle 2ty\sqrt{1-t^2-y^2} - y(3-y^2)\arcsin\frac{t}{\sqrt{1-y^2}}+2\arctg\frac{ty}{\sqrt{1-t^2-y^2}}-\right.\right.\\
&\left. \left.-\displaystyle 2tx\sqrt{1-t^2-x^2} - x(3-x^2)\arcsin\frac{t}{\sqrt{1-x^2}}+2\arctg\frac{tx}{\sqrt{1-t^2-x^2}}+ 6xyt\right]\right|\limits_{z}^{\sqrt{1-x^2-y^2}}=\\
=&\displaystyle\frac{\sqrt{r^2-x_0^2-y_0^2}}{6}\left(2r^2+x_0^2+y_0^2\right)\left(\frac{\pi}{2} - \arcsin\frac{y_0}{\sqrt{x_0^2+y_0^2}}-\arcsin\frac{x_0}{\sqrt{x_0^2+y_0^2}}\right)-\\
&-\displaystyle\frac{z_0}{6}\left(3r^2-z_0^2\right)\left(\frac{\pi}{2} - \arcsin\frac{y_0}{\sqrt{r^2-z_0^2}}-\arcsin\frac{x_0}{\sqrt{r^2-z_0^2}}\right)-\\
&-\displaystyle\frac{y_0}{6}\left(3r^2-y_0^2\right)\left(\arcsin\frac{\sqrt{r^2-x_0^2-y_0^2}}{\sqrt{r^2-y_0^2}}-\arcsin\frac{z_0}{\sqrt{r^2-y_0^2}}\right) -\\
&-\displaystyle\frac{x_0}{6}\left(3r^2-x_0^2\right)\left(\arcsin\frac{\sqrt{r^2-x_0^2-y_0^2}}{\sqrt{r^2-x_0^2}} -\arcsin\frac{z_0}{\sqrt{r^2-x_0^2}}\right)+\\
&+\displaystyle \frac{r^3}{3}\left(\arctg\frac{y_0\sqrt{r^2-x_0^2-y_0^2}}{rx_0} -\arctg\frac{y_0z_0}{r\sqrt{r^2-y_0^2-z_0^2}}\right)+\\
&+\displaystyle \frac{r^3}{3}\left(\arctg\frac{x_0\sqrt{r^2-x_0^2-y_0^2}}{ry_0}-\arctg\frac{x_0z_0}{r\sqrt{r^2-x_0^2-z_0^2}}\right)+\\
&+\displaystyle \frac{x_0 y_0}{3}\sqrt{r^2-x_0^2-y_0^2}+\frac{z_0 y_0}{3}\sqrt{r^2-z_0^2-y_0^2} + \frac{z_0 x_0}{3}\sqrt{r^2-z_0^2-x_0^2}-x_0y_0z_0
\end{array}$$](https://dxdy-01.korotkov.co.uk/f/c/5/3/c539906a5feab81c5551e6703398a75382.png)
Некрасиво и несимметрично. Симметризовать наверняка можно, но мне уже лень. Вопрос закрыт, кому интересно убедиться, что ответ правильный — вот
программка с забитыми формулами и численным взятием интеграла.