Я попытался доказать теорему Больцано-Коши о промежуточном значении функции, но доказательство получилось уж совсем какое-то простое (и не такое, как в учебнике).
Теорема.
Дана функция


и отрезок
![$[a, b] \subset E$ $[a, b] \subset E$](https://dxdy-02.korotkov.co.uk/f/1/7/b/17b560a6777270cb9384a4a5a114535482.png)
. Функция непрерывна на интервале

, непрерывна справа в точке

и непрерывна слева в точке

. На концах отрезка
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
функция принимает значения

и

. Без ограничения общности можно считать, что

. Выберем любое число C принадлежащее интервалу

. Тогда найдется число

такое, что

.
Доказательство.
Я воспользовался методом от противного. Предположим, что существует некоторая функция

, удовлетворяющая всем условиям теоремы, и некоторое число
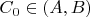
такое, что

выполняется либо
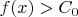
, либо

. На концах отрезка
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
функция так же не принимает значение

, следовательно можно утверждать, что
![$\forall x \in [a, b]$ $\forall x \in [a, b]$](https://dxdy-01.korotkov.co.uk/f/4/5/1/4517c9a2582f1041f05bed238f6061d382.png)
выполняется либо
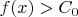
, либо

. Каждой точке
![$x \in [a, b]$ $x \in [a, b]$](https://dxdy-02.korotkov.co.uk/f/d/e/e/dee96e9634467ae09910551cb84f284e82.png)
поставим в соответствие некоторую симметричную окрестность

этой точки, такую что
![$\forall x \in (U_ \varepsilon (x)\cap [a, b])$ $\forall x \in (U_ \varepsilon (x)\cap [a, b])$](https://dxdy-02.korotkov.co.uk/f/5/7/5/5754738684f448b927ac6b265a37f6db82.png)
выполняется одно из двух: либо
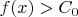
, либо

(это можно сделать, учитывая условия, связанные с непрерывностью функции). Получили бесконечную систему интервалов, покрывающую отрезок
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
. По лемме Бореля-Лебега выберем конечную подсистему, также покрывающую этот отрезок. Здесь надо отметить, что, вообще говоря, в выбранной конечной подсистеме могут встретиться такие две окрестности, одна из которых является собственным подмножеством другой. Удалим из нашей системы все такие "маленькие" окрестности (которые полностью содержатся в некоторой другой). Такая система все равно будет покрывать отрезок. Центры этих окрестностей образуют некоторое конечное подмножество точек из отрезка
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
. Окрестности, которая соответствует меньшей точке, присвоим номер 1. Окрестности, соответствующей точке, которая следует за первой, присвоим номер 2 и так далее. Любые две "соседние" окрестности пересекаются. Более того, если в некоторой точке на пересечении какой-то окрестности и отрезка
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
функция принимает значение, меньшее (большее)

, то и во всех точках на пересечении этой окрестности и отрезка
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
функция будет принимать значения, меньшие (большие)

. Первая окрестность содержит точку

, следовательно
![$\forall x \in (U_1 \cap [a, b])$ $\forall x \in (U_1 \cap [a, b])$](https://dxdy-03.korotkov.co.uk/f/2/8/d/28de437bdd8fd10df1547d184997c8fb82.png)
будет выполняться
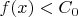
. Вторая окрестность имеет непустое пересечение с первой, следовательно
![$\forall x \in (U_2 \cap [a, b])$ $\forall x \in (U_2 \cap [a, b])$](https://dxdy-01.korotkov.co.uk/f/4/1/7/417d1ba8cf7d1719c712ea2a1fc2fb1882.png)
будет выполняться
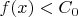
и так далее. Получилось, что, какую бы окрестность
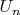
мы бы ни взяли,
![$\forall x \in (U_n \cap [a, b])$ $\forall x \in (U_n \cap [a, b])$](https://dxdy-01.korotkov.co.uk/f/c/5/0/c504fe14e8b3e3c8a16201d674bf048a82.png)
будет выполняться
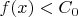
, что очевидно противоречит с тем, что последняя окрестность покрывает точку

и

.
Все верно?