Задача 1.Какова вероятность того что при бросании четырёх кубиков цифры будут идти в убывающем порядке?
Указание.Из каждой такой комбинации перестановками можно получить 24 варианта, где все цифры различны.
Решение.Здесь, конечно, у меня проблема не с классическим определением вероятности, а с подсчетом благоприятных исходов. Мне бы хотелось сделать это максимально строго, а не "на пальцах", так как скорее всего решение последующей задачи будет у меня также базироваться на доказательстве корректности этого решения. И способ решения я хочу использовать именно тот, что идёт в указании к задаче.
Далее под термином последовательность я буду понимать конечную последовательность длины

, которая может состоять только из элементов множества

.
Соответственно количество благоприятных исходов - это количество последовательностей, где цифры идут в убывающем порядке. Раз идут в убывающем - цифры в них точно различны.
Для начала посчитаем общее количество последовательностей из различных цифр. Их

- на первом месте одна из 6 цифр, на втором одна из оставшихся 5, на третьем - одна из оставшихся четырёх и на четвёртом - одна из оставшихся трёх.
Теперь введем множество

- множество последовательностей различных цифр. Как мы сказали,

. Разобьём

на непересекающиеся подмножества, каждое из которых состоит из 24х последовательностей, полученных в результате всевозможных перестановок каких-либо 4х элементов из

.
Каждому из таких подмножеств поставим во взаимно-однозначное соответствие убывающую последовательность.
1.Проверим
однозначность. Возьмём два подмножества,

и

. Если они не равны, то они содержат перестановки цифр, которые отличаются друг от друга хотя бы на 1 цифру каждая. Но тогда им соответствуют и разные убывающие последовательности, отличающиеся хотя бы на

цифру.
2.Проверим
взаимность. Возьмём произвольную убывающую последовательность. Переставив её элементы 24-мя образами, мы получим одно из подмножеств

.
Таким образом, мы установили биекцию между количеством убывающих последовательностей и сконструированных вышеописанным образом подмножеств

.
Значит количество убывающих последовательностей равно
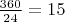
, так как каждое подмножество состоит из

элементов, эти подмножества не пересекаются, а всего элементов во множестве, из которого берем подмножества -

.
Значит искомая вероятность равна

.

.
Прошу проверить, всё ли здесь строго и корректно доказано.
Тот факт, что количество благоприятных исходов -

сомнению не подлежит, так как я проделал решение вторым способом - зарисовкой "дерева вариантов", которое, к сожалению становится слишком огромным во второй задаче. Вследствие чего я и решил вернуться к методу, указанному автором книги.