численное решение ОДУ c "singular point" в Mathematica

[student_kiev]

При решении некой задачи ОТО требуется численно решить следующее нелинейное уравнение:
$\dfrac{dy}{dx} = -\dfrac{x}{y(x)} \dfrac{1- \lambda \sqrt{x^2+y(x)^2(1- \lambda^2 x^2)}}{1-\lambda^2 x^2}$
при граничном условии $y(0)=1$ на отрезке $x \in [0,1]$, при различных значениях параметра $\lambda \in [0,1)$.

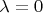
При $\lambda = 0$, естественно, получаем (полу)окружность, что из физической постановки задачи верно. При ненулевых $\lambda$ физически должна получаться вытянутая вдоль $x$ капля. Дальше начинаются танцы с бубеном. Пытаюсь влоб найти численное решение в Mathematica, используя ParametricNDSolve при стандартных настройках:

sol = ParametricNDSolve[{y'[x] == -x/y[x] (1 - \[Lambda] Sqrt[x^2 + y[x]^2 (1 - \[Lambda]^2 x^2)])/(1 - \[Lambda]^2 x^2), y[0] == 1}, y, {x, 0, 2}, {\[Lambda]}]
Plot[Evaluate[Table[y[\[Lambda]][x] /. sol, {\[Lambda], 0.1, 0.995, .2}]], {x, 0, 1}, PlotRange -> All]

но, понятное дело, там, где капля пересекает ось $x$ производная $y'(x)$ обращается в бесконечность, так что NDSolve загибается (интересно, что случай с окуржностью он решает, хотя там тоже бесконечности вылезают).

Вобщем вопрос: какие есть подходы к численному решению такой задачи? Можно, конечно, в ряд разложить в окрестности особой точки, но неужели стандартными методами Mathematica такие задачи не решаются?

[alisa-lebovski]

Попробуйте перейти к полярным координатам.

[Markiyan Hirnyk]

Вопрос относится к разделу "Околонаучный софт".

Цитата:

При ненулевых $\lambda$ физически должна получаться вытянутая вдоль $x$ капля

мне непонятно.
Вы не упомянули ошибок типа

At x == 1.0526797499069145`, step size is effectively zero; \
singularity or stiff system suspected.

пр выполнении Вашего кода.

[Vince Diesel]

Так у вас $x$ только до единицы. Вот так она что-то считает:

sol = ParametricNDSolve[{y'[x] == -x/  y[x] (1 - \[Lambda] Sqrt[x^2 + y[x]^2 (1 - \[Lambda]^2 x^2)])/(1 - \[Lambda]^2 x^2), y[0] == 1}, y, {x, 0, 2}, {\[Lambda]}]
Plot[Evaluate[Table[UnitStep[y[\[Lambda]][x]] y[\[Lambda]][x] /. sol, {\[Lambda],  0.1, 0.995, .2}]], {x, 0, 3}, PlotRange -> All]

Команда UnitStep здесь, чтобы обрезать быстро убывающую отрицательную часть решения.

[student_kiev]

всем спасибо, все решилось обрезанием отрицальной части решения (с последующей сшивкой зеркального отображения в горизонтальной оси), а NDSolve, на самом деле, все решала с самого начала правильно