Не знай, может и ошибся где-то.
(6-, 5- и 4-наборы прогрессий)
[7, 37, 67, 97, 127, 157]
[107, 137, 167, 197, 227, 257]
[359, 389, 419, 449, 479, 509]
[11, 71, 131, 191, 251, 311]
[53, 113, 173, 233, 293, 353]
[13, 103, 193, 283, 373, 463]
[5, 11, 17, 23, 29]
[5, 17, 29, 41, 53]
[11, 41, 71, 101, 131]
[37, 67, 97, 127, 157]
[137, 167, 197, 227, 257]
[151, 181, 211, 241, 271]
[277, 307, 337, 367, 397]
[389, 419, 449, 479, 509]
[401, 431, 461, 491, 521]
[5, 47, 89, 131, 173]
[5, 53, 101, 149, 197]
[43, 103, 163, 223, 283]
[71, 131, 191, 251, 311]
[113, 173, 233, 293, 353]
[61, 151, 241, 331, 421]
[83, 173, 263, 353, 443]
[89, 179, 269, 359, 449]
[103, 193, 283, 373, 463]
[5, 101, 197, 293, 389]
[29, 149, 269, 389, 509]
[5, 131, 257, 383, 509]
[11, 17, 23, 29]
[41, 47, 53, 59]
[61, 67, 73, 79]
[251, 257, 263, 269]
[7, 19, 31, 43]
[17, 29, 41, 53]
[47, 59, 71, 83]
[127, 139, 151, 163]
[227, 239, 251, 263]
[257, 269, 281, 293]
[397, 409, 421, 433]
[467, 479, 491, 503]
[5, 23, 41, 59]
[43, 61, 79, 97]
[53, 71, 89, 107]
[113, 131, 149, 167]
[313, 331, 349, 367]
[59, 83, 107, 131]
[79, 103, 127, 151]
[349, 373, 397, 421]
[419, 443, 467, 491]
[13, 43, 73, 103]
[23, 53, 83, 113]
[41, 71, 101, 131]
[67, 97, 127, 157]
[167, 197, 227, 257]
[181, 211, 241, 271]
[307, 337, 367, 397]
[349, 379, 409, 439]
[419, 449, 479, 509]
[431, 461, 491, 521]
[31, 67, 103, 139]
[241, 277, 313, 349]
[281, 317, 353, 389]
[311, 347, 383, 419]
[47, 89, 131, 173]
[67, 109, 151, 193]
[97, 139, 181, 223]
[107, 149, 191, 233]
[157, 199, 241, 283]
[227, 269, 311, 353]
[317, 359, 401, 443]
[337, 379, 421, 463]
[13, 61, 109, 157]
[53, 101, 149, 197]
[83, 131, 179, 227]
[5, 59, 113, 167]
[19, 73, 127, 181]
[29, 83, 137, 191]
[239, 293, 347, 401]
[379, 433, 487, 541]
[19, 79, 139, 199]
[47, 107, 167, 227]
[103, 163, 223, 283]
[131, 191, 251, 311]
[137, 197, 257, 317]
[151, 211, 271, 331]
[173, 233, 293, 353]
[277, 337, 397, 457]
[31, 97, 163, 229]
[41, 107, 173, 239]
[241, 307, 373, 439]
[251, 317, 383, 449]
[7, 79, 151, 223]
[67, 139, 211, 283]
[167, 239, 311, 383]
[23, 101, 179, 257]
[73, 151, 229, 307]
[113, 191, 269, 347]
[233, 311, 389, 467]
[5, 89, 173, 257]
[29, 113, 197, 281]
[149, 233, 317, 401]
[179, 263, 347, 431]
[11, 101, 191, 281]
[47, 137, 227, 317]
[151, 241, 331, 421]
[173, 263, 353, 443]
[179, 269, 359, 449]
[193, 283, 373, 463]
[277, 367, 457, 547]
[71, 167, 263, 359]
[101, 197, 293, 389]
[7, 109, 211, 313]
[47, 149, 251, 353]
[127, 229, 331, 433]
[23, 131, 239, 347]
[163, 271, 379, 487]
[223, 331, 439, 547]
[79, 193, 307, 421]
[37, 157, 277, 397]
[71, 191, 311, 431]
[73, 193, 313, 433]
[107, 227, 347, 467]
[149, 269, 389, 509]
[11, 137, 263, 389]
[31, 157, 283, 409]
[41, 167, 293, 419]
[101, 227, 353, 479]
[131, 257, 383, 509]
[5, 137, 269, 401]
[47, 179, 311, 443]
[67, 199, 331, 463]
[73, 211, 349, 487]
[29, 173, 317, 461]
[7, 157, 307, 457]
[13, 163, 313, 463]
[17, 167, 317, 467]
[73, 223, 373, 523]
[41, 197, 353, 509]
[43, 211, 379, 547]
[19, 193, 367, 541]
(gp-code)
Код:
A= []; so= 0;
for(d=2, 544,
for(i=2, 100,
p= prime(i);
P= concat([], [p]); \\print(d" "p" "P);
while(p+d<=547,
p= p+d; \\print1(p", ");
if(isprime(p), P= concat(P, [p]), break())
);
if(#P>1, A= concat(A, [P]));
)
);
print(#A"\n");
n6=n5=n4=n3=n2=0;
for(i=1, #A,
if(#A[i]==6, n6++);
if(#A[i]==5, n5++);
if(#A[i]==4, n4++);
if(#A[i]==3, n3++);
if(#A[i]==2, n2++);
);
print(n6" "n5" "n4" "n3" "n2"\n");
forstep(l=6,4,-1,
for(i=1, #A,
if(#A[i]==l, print(A[i]))
); print()
);

 прогрессий длины
прогрессий длины  прогрессия длины
прогрессия длины  ,
,  прогрессий длины
прогрессий длины  ?
? , а не
, а не 










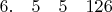









![$[37, 67, 97, 127, 157]$ $[37, 67, 97, 127, 157]$](https://dxdy-03.korotkov.co.uk/f/e/5/3/e532c97e05507bc91fc1ce7ea18a47d382.png) это шестёрка
это шестёрка ![$[7, 37, 67, 97, 127, 157] $ $[7, 37, 67, 97, 127, 157] $](https://dxdy-03.korotkov.co.uk/f/6/8/c/68c02a71ed2ca91c5feef7143caeb75782.png) от которой почему-то отрезано первое простое, то бишь
от которой почему-то отрезано первое простое, то бишь  .
. , где
, где  - переменная, соответствующая
- переменная, соответствующая  -му простому числу, а
-му простому числу, а  - переменные, соответствующие прогрессиям, в которые это число входит.
- переменные, соответствующие прогрессиям, в которые это число входит. - мы платим по
- мы платим по  за каждую взятую прогрессию, и по
за каждую взятую прогрессию, и по  за каждое непокрытое число (т.к. мы сможем непокрытые числа покрывать по два).
за каждое непокрытое число (т.к. мы сможем непокрытые числа покрывать по два).