Можно ли как то просто параметризовать семейство эллипсов (хотелось бы получить параметрические уравнения семейства), которое получается когда один катится вокруг второго покоящегося, такого же размера, как первый. Если начальное положение таково, что эллипсы симметричны относительно общей касательной - то нарисовать все просто (хотя получить уравнение огибающей не удалось - там почти окружности вроде - наверное какая-то кривая четвертого порядка). Сложно если начальное положение несимметрично.
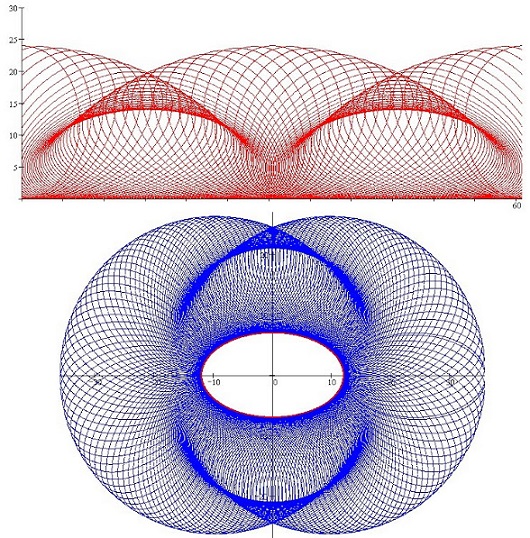
Для случая - когда эллипс катится по плоскости - тоже не просто получить параметрическое семейство - интеграл по длине дуги все портит.
И такой вопрос в каком случае, заметаемая площадь больше -
1. эллипс катится вдоль прямолинейного отрезка с длиной равной длине эллипса,
2. катится вдоль совпадающего с ним эллипса?