Строго верные цифры

[Heathy]

В учебнике Алимова "Алгебра 8 класс" приводится такое определение:

Цитата:

если граница абсолютной погрешности не превос­ходит половины единицы разряда, следующего за разрядом рассматриваемой цифры, то эту цифру в записи приближенного значения числа называют строго верной.

Далее приводится пример:

Цитата:

если $ x = 4,056 ± 0,0005$, то все цифры в записи приближенного значения $4,056$ будут стро­го верными, так как граница абсолютной погрешности (т. е. число $0,0005$) не превосходит половины единицы последнего разряда числа $4,056$, т. е. не превосходит $0,001$.

Я правильно понимаю, что тут ошибка? Строго верными можно считать только все цифры кроме 6, она будет просто верной. Ведь ее разряд $0,001$ , единица следующего разряда $0,0001$ , а половина этой единицы это $0,00005$ .

[arseniiv]

Тут ошибка в «т. е. не превосходит $0{,}001$» — это же и есть последний разряд, а не его половина, которая будет здесь удачным образом равна границе абсолютной погрешности, а потому и не превосходить её. Чуть только мы прибавим к нашей границе что-то ещё, цифра 6 перестанет быть строго верной.

[Heathy]

arseniiv в сообщении #1403559 писал(а):

Тут ошибка в «т. е. не превосходит $0{,}001$» — это же и есть последний разряд, а не его половина, которая будет здесь удачным образом равна границе абсолютной погрешности, а потому и не превосходить её. Чуть только мы прибавим к нашей границе что-то ещё, цифра 6 перестанет быть строго верной.

Но ведь в определении строго верной цифры фигурирует не половина единицы разряда рассматриваемой цифры, а половина единицы разряда, следующего за разрядом рассматриваемой цифры.

[arseniiv]

Посмотрел 19-е издание, вроде проблема с самим определением строго верной цифры. Когда рассматривается два подобных определения, одно пошире и другое поуже, то широкое требует погрешности не больше единицы рассматриваемого разряда, а узкое — не больше половины единицы рассматриваемого разряда.

(У этого есть наглядная иллюстрация)

Точное значение ближе к своим приближениям с $n$ строго верными цифрами, чем ко всем иным приближениям с $n$ значащими цифрами; притом оно вообще имеет больше одного — два — таких приближения только когда находится на полпути, в остальных случаях приближение со всеми $n$ строго верными цифрами ровно одно.

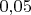
А вот требовать не больше $0{,}05$ единицы рассматриваемого разряда (половину единицы следующего) — это слишком строго и противоречит в том числе и заявлению из учебника, что правило округления даёт все строго верные цифры (оно не даёт такой точности).

-- Сб июл 06, 2019 17:41:25 --

В частности можно посмотреть на книгу Демидовича, Марона «Основы вычислительной математики», гл. 1 §3. Там тоже приводятся и узкое, и широкое определения.

[Heathy]

Получается, если вычеркнуть из определения слова ", следующего за разрядом " , то все встает на свои места. Странно, что в учебнике с таким большим количеством переизданий это не исправлено.

[arseniiv]

Может, в новых изданиях?.. Сейчас школьные учебники так часто переиздаются, что легко попадаются разные издания, если только у школьной библиотеки не достаточно денег, чтобы постоянно обновлять все книги. Может быть интересно проверить, с какого издания эта ошибка существует — она могла быть добавлена, а не иметься изначально, и такое бывает. (О причинах можно только гадать, если это не банальная ошибка редактирования — меняешь фразу, забываешь кусок старой, поправляешь синтаксис и получается такое.)

[Heathy]

У меня 18-е издание 2011 года.