Как получается функция вероятности?

[AnthonyP]

Есть функция потерь:
$\Phi(u,x)=\left\{ \begin{array}{rcl} \left\lvert u+ x \right\rvert, \left\lvert u+ x \right\rvert<1& \\ 2, \left\lvert u+ x \right\rvert \geqslant 1&\\ \end{array} \right.$
И функция распределения случайной величины $x$:
$F(x)=\left\{ \begin{array}{rcl} 0, x\leqslant-1& \\ \frac{x+1}{4}, \left\lvert x \right\rvert < 1& \\ 1, x\geqslant 1& \\ \end{array} \right.$
В задаче находится $P_{1}=P \left\lbrace x: \varphi(u,x)\leqslant 1 \right\rbrace$
И после этого сразу дается ответ со словами "Нетрудно найти...":
$P_{1}=\left\{ \begin{array}{rcl} 0, \left\lvert u \right\rvert \geqslant 2 & \\ \frac{u+2}{4}, -2 \leqslant u \leqslant 0& \\ 1-\frac{u}{4}, 0< u < 2& \\ \end{array} \right.$
Но я не понял этого. Хочу воспользоваться определением:
$P \left\lbrace x: x \leqslant y \right\rbrace = F(y)$
Получается, что нужно каким-то образом подставить $\Phi$ в $F(x)$, на этом этапе и появились трудности. Как это сделать?

[Lia]

AnthonyP в сообщении #1398681 писал(а):

И функция распределения случайной величины $x$:

Какой случайной величины? Это величина чего?

[teleglaz]

AnthonyP в сообщении #1398681 писал(а):

В задаче находится $P_{1}=P \left\lbrace x: \varphi(u,x)\leqslant 1 \right\rbrace$

Сдаётся мне фи то должно большим быть? А?

AnthonyP в сообщении #1398681 писал(а):

И после этого сразу дается ответ со словами "Нетрудно найти...":
$P_{1}=\left\{ \begin{array}{rcl} 0, \left\lvert u \right\rvert \geqslant 2 & \\ \frac{u+2}{4}, -2 \leqslant u \leqslant 0& \\ 1-\frac{u}{4}, 0< u < 2& \\ \end{array} \right.$
Но я не понял этого.

Вы точно правильно переписали? По мне как по другому должно быть.

[valerych]

AnthonyP в сообщении #1398681 писал(а):

Есть функция потерь:
$\Phi(u,x)=\left\{ \begin{array}{rcl} \left\lvert u+ x \right\rvert, \left\lvert u+ x \right\rvert<1& \\ 2, \left\lvert u+ x \right\rvert \geqslant 1&\\ \end{array} \right.$
И функция распределения случайной величины $x$:
$F(x)=\left\{ \begin{array}{rcl} 0, x\leqslant-1& \\ \frac{x+1}{4}, \left\lvert x \right\rvert < 1& \\ 1, x\geqslant 1& \\ \end{array} \right.$
В задаче находится $P_{1}=P \left\lbrace x: \varphi(u,x)\leqslant 1 \right\rbrace$

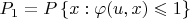
Это ведь задача из книжки Малышева, Кибзуна. Там ответ неправильно приведён. Посмотрите книжку Кибзуна, Кана "Задачи стохастического программирования с вероятностными критериями", пример 2.3. Там тот же пример, но с правильным ответом.
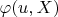
Чтобы получить ответ, подставьте в функцию вероятности $P_1(u)$ функцию $\Phi(u, X)$ (не $\varphi(u, X)$, как написано у Вас), раскройте модуль и примените формулу для вычисления вероятности попадания случайной величины в интервал.