1. Можно сделать по "общей теории"...Пусть

- гамильтоново векторное поле с гамильтонианом

, тогда поле это - с нулевой дивергенцией. Из условий задачи следует, что его особая точка 0 - невырождена, седловая. По теореме Брюно (1972, конец статьи про гамильтоновы векторные поля) поле

приводится к резонансной гамильтоновой нормальной форме

формальным каноническим преобразованием (и оно будет аналитическим , ибо выполняется "условие А" Брюно. А можно сослаться на теорему Рюссмана, которая приводится там же. Или на следствие из нее, там же, стр. 228. Про наш случай там сказано, что это сделал Ляпунов в 1892). При этом старый гамильтониан станет (в новых координатах
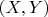
) "резонансным" - т.е., будет зависеть лишь от резонансной переменной

, что и требовалось.
Но так - неинтересно. А интересно - ручками...
-- 07.06.2019, 02:11 --2. Задача фактически состоит в одновременной нормализации пары

, где

- стандартная симплектическая структура. Выше
scwec нормализовал компоненту

- по лемме Морса привел ее к виду

(но испортил симплектическую структуру. Пусть она стала равной

, G(0,0)

). Будем искать замену

, исправляющую с.с. ,в виде

, где

,

(первая переводит гиперболы - линии уровня

- в себя, вторая - переставляет их ). Якобиан этой замены (считаем явно) равен

,

где

.

С.с. поправится, если это произведение

равно

.
Разложим аналитическую функцию

в ряд

, и разобьем сумму на два слагаемых

: в первую сумму
включим мономы, для которых

, во вторую - остальные. Полагая

, из

, интегрируя, найдем

. Заметим, что для частного

справедливо

. Поэтому уравнение

(приравняем якобиан к

) сводится к уравнению

, которое явно решается:
если

, то

(деление не попортило радиуссы сходимости )
Уф, с.с. исправлена. Осталось заметить, что (специфический вид замены) в новых координатах

как раз и будет равна

(да?), и будет зависить лишь от

. Всё!