не имеющего счётной базы (как прямая

, например)
Числовая прямая со стандартной топологией имеет счётную базу.
Сеть топологического пространства

- семейство подмножеств (необязательно открытых, в отличие от базы!!!) множества

, таких, что каждое открытое в

множество можно представить в виде объединения некоторого числа элементов этого семейства.
Правильно. Теперь докажите, что топологическое пространство со счётной сетью сепарабельно. Если Вы умеете доказывать аналогичное утверждение для счётной базы, то проблемы у Вас не должно возникнуть.
пространство

рациональных чисел не подходит - оно счётно, но его вес тоже счётен
Конечно, не подходит. Пространство, которое я имел в виду, устроено проще. Это просто сходящаяся последовательность вместе с предельной точкой, и к каждой точке этой последовательности "прицеплена" ещё одна сходящаяся последовательность. Например, так. Рассмотрим на плоскости (с системой координат

) множество

, являющееся объединением следующих подмножеств (я для удобства считаю, что натуральный ряд

не содержит нуля; если Вы считаете иначе, просто замените во всяких дробях знаменатель

на

и т. п.):
1) точка

;
2) множество

, где
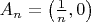
;
3) множества

,

, где

.
Базу топологии образуют множества следующих видов:
1) одноточечные множества

,

;
2) множества

,

(последовательность, сходящаяся к

, вместе с предельной точкой

);
3) множества

, где

— последовательность натуральных чисел.
Схема доказательства.
1) Доказать, что пространство

является объединением двух подпространств счётного веса (в качестве этих подпространств можно взять

и

; Вам нужно доказать, что эти подпространства имеют счётный вес).
2) Доказать следующую лемму: если задано счётное множество последовательностей натуральных чисел

,

, то существует последовательность натуральных чисел

, растущая быстрее их всех, то есть, например, удовлетворяющая неравенствам

для всех

и всех
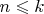
.
3) Используя указанную лемму, доказать, что пространство

не имеет счётной базы.