Прошу проверить решение.
Задача:Найти все значения

при которых равен двум ранг матрицы:
 Решение:
Решение:Раз ранг матрицы равен двум, то это значит что можно умножить вторую строку на некоторое число

и сложить с третьей строкой, умноженной на некоторое число

, и получить первую строку. Исходя из этих соображений составляю систему уравнений:

Из первого и второго уравнения получаю что

и

. Эти значения подставляю в третье уравнение:

. Корни этого уравнения:

и
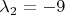
.
Проверка для

:

Значит,

не подходит.
Проверка для
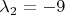
:


Подходит.
Ответ: Под искомые требования подходит только

.