Покажем, как задача может быть сведена к частному случаю, в котором участвуют не функции, а только числа. Ход рассуждений несколько экзотический. Я вообще не собирался писать, тем более и до конца не дорешал, но сегодня наткнулся на
эту тему. (Вероятно,
arqady имел в виду какой-то изящный элементарный ход решения, а предлагаемый --- тупо технический. Пардон.)
1) Ясно, что можно предполагать

. Кроме того, аффинным преобразованием аргумента можно привести к случаю
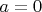
,

.
2)

--- выпуклая функция, определенная на
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
. Из общих свойств выпуклых функций следует, что

непрерывна во внутренних точках, и также можем считать, что и в граничных точках

,

тоже. Короче,

непрерывна на
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
.
3) Опять-таки из общих свойств выпуклых функций, для любого
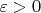
можно найти кусочно-линейную выпуклую функцию

такую, что

всюду на
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
. Поэтому исходное неравенство достаточно доказать для кусочно линейных (в общей теории такие называются "полиэдральные", а тут можно сказать "полигональные") выпуклых функций.
4) Вычитая из

подходящую линейную функцию, можно считать, что

. Таким образом,

всюду на
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
.
5) Для

введем "функцию Грина"

при

, и

при

.
Т.е.

при

,

при

, а на отрезках
![$[0,t]$ $[0,t]$](https://dxdy-02.korotkov.co.uk/f/9/9/0/990afe3dc2a01ee124e9c8ef79e63b2182.png)
и
![$[t,1]$ $[t,1]$](https://dxdy-04.korotkov.co.uk/f/3/c/e/3ce638dd136b840d5faff44334c1370882.png)
линейная. Ясно, что

выпукла по

на
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
.
Предложение. Пусть  --- выпукла на
--- выпукла на ![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png) , кусочно-линейная,
, кусочно-линейная,  ,
,  . Тогда
. Тогда  представляется как положительная линейная комбинация
представляется как положительная линейная комбинация

для некоторых  ,
,  . Доказательство.
. Доказательство. Поскольку

--- кусочно-линейна и выпукла, то существуют точки

, такие, что на каждом из отрезков
![$[t_i, t_{i+1}]$ $[t_i, t_{i+1}]$](https://dxdy-04.korotkov.co.uk/f/f/4/f/f4ff2ed1e9bf6d009482f15043a4192e82.png)

линейна. На этих отрезках производная

постоянна, а в точке

делает скачок, причем величина этого скачка

положительна. Таким образом,

является решением диффуравнения

с краевыми условиями

. Остается заметить, что функция

является решением уравнения

,

, с

. Значит

 Замечание.
Замечание. Конечно, легко дать доказательство предложения, и не поминая дельта-функции. Но исходно я это решал именно так.
Вывод: достаточно утверждение задачи доказать лишь для случая функций

.