Тема меня не отпускает. Если Гильбертово пространство это обобщение Евклидова (так стоит в википедии), как далеко можно распространять геометрическую интуицию на такое пространство?
Вот пример. В евклидовой геометрии сумма углов треугольника равна
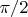
. Я взял три функции

,

,

и на интервале
![$[0, 1]$ $[0, 1]$](https://dxdy-03.korotkov.co.uk/f/e/8/8/e88c070a4a52572ef1d5792a341c090082.png)
вычислил углы. Сумма углов получилась больше
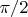
.
Потом я взял вопрос ещё абстрактнее. Определим сферу, как множество точек равноудалённых от заданной. Взяв точку на этой сфере, противостоит ли ей через диаметр ровно одна точка? Я взял

в центре сферы,

с одного краю и ищу

такую, 1) что она лежит от

на том же расстоянии, что и

, то есть

и 2) что угол между радиусами равнен нулю

. Получил не одну

, а множество, с единственным ограничением по норме.
Собственно вопрос: в каком смысле Гильбертово пространство является обощением для Евклидова? Спасибо!