Даны две 2-плоскости имеющие только одну общую точку находящиеся в четырехмерном евклидовом пространстве. Доказать, что существует 2-плоскость, которая пересекает эти плоскости по прямым и при этом перпендикулярна этим данным плоскостям в 3-х мерном смысле перпендикулярности плоскостей.
Решение можно найти в учебниках по четырехмерной геометрии, например, за авторством Смировой И.М. и Смирнова В.А.: «Пусть

и

две плоскости, имеющие одну общую точку

. Через точку

проведем два пространства, перпендикулярные плоскостям

и

, соответственно. Их пересечением будет искомая плоскость

, перпендикулярная этим плоскостям».
Это доказательство не доказательство, т.к. плоскость

может пересекать

и

в их общей точке

и не иметь с этими плоскостями больше никаких других общих точек, кроме точки

, а следовательно,

не будет искомой плоскостью. Кроме того, если пространство перпендикулярно плоскости это еще не значит, что любая плоскость, заключенная в этом пространстве, будет перпендикулярна исходной плоскости.
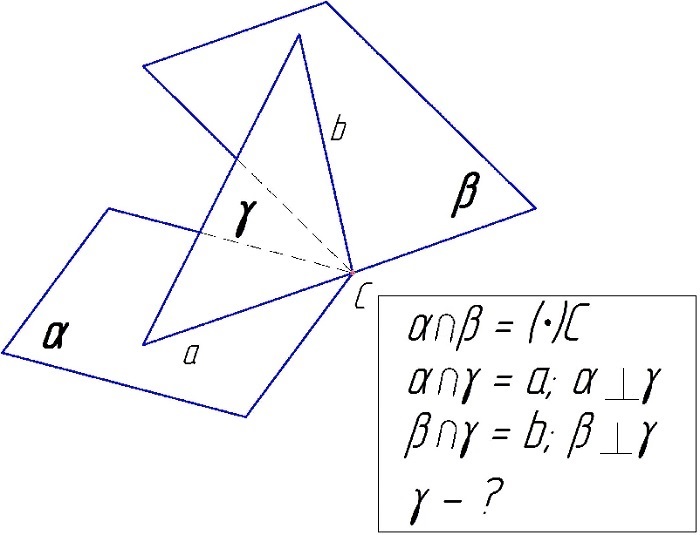
Пусть

и

две плоскости, имеющие одну общую точку

. Через точку

проведем два пространства

и

, перпендикулярные плоскостям

и

, соответственно . Пространство

пересечет плоскость

по прямой

, а плоскость

по прямой

. Пространство

пересечет плоскость

по прямой

, а плоскость

по прямой

. Пространство

пересечется с пространством

по плоскости

. Плоскость

будет искомой лишь в том случае, если прямая

совпадет с прямой

и вместе с тем прямая

совпадет с прямой

. Но из чего следует обязательность или хотя бы возможность такого совпадения не ясно. Поэтому я и утверждаю, что это доказательство не доказывает данной теоремы.
Некоторые отправные сведения для доказательства теоремы:
1) Если два различных пространства имеют общую точку, то они пересекаются по плоскости.
2) Если плоскость не лежит в пространстве и имеет с этим пространством общую точку, то она пересекает пространство по прямой.
3) По определению плоскость

, пересекающая пространство

, по прямой

, называется перпендикулярной пространству

, если она перпендикулярна любой плоскости, лежащей в этом пространстве и проходящей через прямую

.
4) Признак перпендикулярности плоскости и пространства: Если плоскость проходит через прямую перпендикулярную пространству, то такие плоскость и пространство взаимно перпендикулярны. Итак, проведем через любую точку плоскости пучок прямых лежащих в этой плоскости. К каждой прямой пучка проведем пространство перпендикулярное этой прямой. Такое пространство единственно(что доказывается в этой же книжке). Каждое такое пространство будет перпендикулярно данной плоскости. Но совпадать эти пространства не могут, т.к. в противном случае через точку пространства будет проходить не единственный перпендикуляр к нему. Значит утверждение(Через любую точку гиперпространства проходит единственное пространство, перпендикулярное данной плоскости) не верно.