Это место надо потщательней почитать. Может быть, у них буковка меняет смысл. Или, скажем, в начале можно считать, что
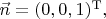
а потом - что это некий фон, хотя и не вакуум, и над ним дальше рассматривают возмущения.
Во-первых, я сверху слегка ошибся -- потерял мнимую единицу перед
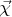
, то есть параметризация на самом деле имеет вид:
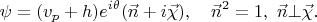
Во-вторых, я ещё раз перечитал этот кусок и пока что по-прежнему не вижу, где затерялся вакуум
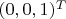
, поскольку и

, и
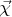
у них являются динамическими полями. По сути, можно сверится даже с их ответом, поскольку после подстановки этой параметризации они интегрируют по

и
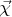
, получая некоторый эффективный лагранжиан. Постараюсь провести эти выкладки сам в ближайшем будущем, как время чуть побольше будет. Наконец, надо отметить, что с точки зрения числа степеней свободы вроде всё чисто: изначально было
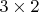
штук, в параметризации же по одной от

и

, по три от

и
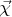
, минус две из-за наличия двух связей, то есть тоже

. В этом смысле вопрос только в том, куда потерялся вакуум.
Про ферромагнетизм я просто не в курсе

Подождите твердотельщиков.
Это просто другое нарушенное состояние для того же лагранжиана:
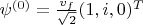
. В этом случае они предлагают использовать
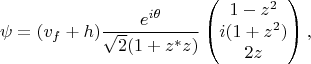
где

-- комплексное поле. Здесь уже вакуум отчётливо виден, но при этом меня несколько настораживает, что число степеней свободы "проседает": их в этой параметризации всего

.
Честно говоря, не очень понимаю даже, чем одна параметризация лучше или хуже другой. Надо следить за особыми точками, и всё. Ну и линеаризациями заниматься аккуратно.
Насколько я могу понять, здесь всё из-за отсутствия Лоренц-инвариантности. Из-за этого "наивная" теорема Голдстоуна перестаёт работать. Число голдстоуновских мод уже не есть
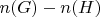
, как обычно, а может быть и меньше. Поэтому, видимо, и стандартная параметризация не работает так, как надо, так что приходится прибегать к каким-то геометрическим рассуждениям. В общем, в статье авторы как раз всё это тщательно и исследуют.
Из второй статьи вы привели хорошую цитату, которая мне понятна (и я бы, может, взялся её пересказать). Может, вы достаточно большую "геометрическую" цитату приведёте из первой статьи, с которой начали тему?
Там в конце есть параграф
Underlying geometry, который я и привожу ниже:
Цитата:
Having demonstrated our theorem (см. ниже) at work in very different examples, we now study the underlying geometry. Usually, canonically conjugate pairs in mechanics (such as type B NGBs) imply a
symplectic structure mathematically, which requires an even-dimensional manifold

, and if closed, a nontrivial second de Rham cohomology
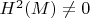
. However, we have seen in the last two examples that type A and type B NGBs can coexist on an odd-dimensional

with
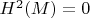
. This puzzle can be solved as follows.
The time integral of the first term in
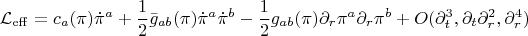
defines a one-form
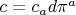
on the coset space, and its exterior derivative gives a closed two-form
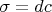
. Using the coordinates in

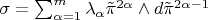
for

type B NGBs, which resembles a symplectic two-form. However, type A NGB fields for the remaining
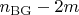
broken generators do not have terms with first order in time derivatives, and hence do not take part in

. Therefore,

has a constant rank but is degenerate, and hence is not a symplectic structure in the usual sense.
This kind of a partially symplectic (or
presymplectic) structure is possible on a coset space by considering the following fiber bundle,
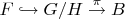
, where the base space
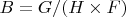
is symplectic. The fiber

is a subgroup of

that commutes with

. The symplectic structure

on

is pulled back to

as
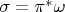
. Since
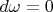
on

implies
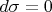
on

, we can always find a one-form

such that
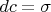
locally on

, which appears in
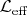
. Type B NGBs live on the symplectic base manifold

, whose coordinates form canonically conjugate pairs, while the type A NGBs live on the fiber

, each coordinate representing an independent NGB. The type A and type B NGBs can coexist on

in this fashion.
The Heisenberg ferromagnetic model has the coset space
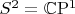
which is Kähler and hence symplectic, with one type B NGB. On the other hand, the spinor BEC example in its ferromagnetic state has
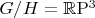
which is not symplectic. The last term in
![$$\mathcal{L}_{\mathrm{eff}} = \hbar v^2_f i \frac{z^* \dot{z} - \dot{z}^* z}{1+z^{*} z} + \frac{\hbar^2}{\lambda} \left( \dot{\theta} -i \frac{z^{*} \dot{z} - \dot{z}^{*} z}{1 + z^{*} z}\right)^2 - \frac{\hbar^2 v^2_f}{2m} \left[ \left(\partial_r \theta -i \frac{z^{*} \partial_r{z}-\partial_r{z}^{*} z}{1+z^* z}\right)^2 + \frac{2\partial_r z^* \partial_r z}{(1+z^* z)^2}\right]$$ $$\mathcal{L}_{\mathrm{eff}} = \hbar v^2_f i \frac{z^* \dot{z} - \dot{z}^* z}{1+z^{*} z} + \frac{\hbar^2}{\lambda} \left( \dot{\theta} -i \frac{z^{*} \dot{z} - \dot{z}^{*} z}{1 + z^{*} z}\right)^2 - \frac{\hbar^2 v^2_f}{2m} \left[ \left(\partial_r \theta -i \frac{z^{*} \partial_r{z}-\partial_r{z}^{*} z}{1+z^* z}\right)^2 + \frac{2\partial_r z^* \partial_r z}{(1+z^* z)^2}\right]$$](https://dxdy-02.korotkov.co.uk/f/9/e/a/9ea5f935bc24e42cd7be43e6c1c046ff82.png)
is nothing but the Fubini--Study metric on
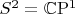
which is Kähler and hence symplectic. The first term in
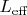
defines the one-form

whose exterior derivative
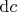
gives precisely the Kähler form associated with the metric up to normalization. However

is an orthogonal direction with no connection to the symplectic structure. We can define the projection
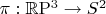
simply by eliminating the

coordinate. It shows the structure of a fiber bundle
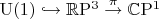
, which is the well-known Hopf fibration (the difference between

and
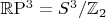
is not essential here). The phonons in the magnetic field also show a partially symplectic structure.
In fact, it is always possible to find such a symplectic manifold

if

is compact and semisimple, thanks to Borel's theorem. Generalizations to non-semi-simple groups would be an interesting future direction in mathematics.
Теорема писал(а):
Пусть
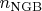
-- число намбу-голдстоуновских бозонов, а
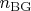
-- число сломанных генераторов. Тогда
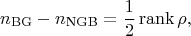
где
![$$\rho_{ij} \equiv \lim_{\Sigma \to \infty} \frac{-i}{\Omega} \langle 0 | [Q_i,Q_j] | 0 \rangle.$$ $$\rho_{ij} \equiv \lim_{\Sigma \to \infty} \frac{-i}{\Omega} \langle 0 | [Q_i,Q_j] | 0 \rangle.$$](https://dxdy-01.korotkov.co.uk/f/4/b/0/4b011f2c238bc07c1174eead7c0c977b82.png)
Здесь
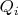
-- генераторы (полной) симметрии, а

-- пространственный объём системы.
Контекст я постарался восполнить, насколько смог, но всё же может быть проблемным восприятие. Подробности можно найти в статье. Та, что из оригинального сообщения в теме, к слову, всего

страниц (в PRL была опубликована) и доступна в arXiv. Вторая статья -- гораздо более объёмная (
страниц где-то), но там, как понимаю, тонкости теоремы и геометрических построений рассказаны в деталях.