Я, конечно, могу ошибаться (потому и спрашиваю), но мне не очевидно, что "возможность возвращаться" в лемме о ниме с увеличениями нигде не вступает в противоречие с утверждением "мы в самом деле всегда можем сделать такой ход, чтобы осталось нечётное число кучек размера 1, т.е. приведём соперника к поражению".
А если переходы-возвраты возможны, но не с той чётностью, которая нам нужна?
И разве единственная игра

с

не может распасться в сумму двух игр
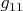
,

, таких, что

? Получаем, что

,

, и это что -- ход из проигрышной в проигрышную? Откуда именно следует, что теперь это нормально? Насколько понимаю, для именно нима, где нет увеличений, такого контрпримера (или подобия контрпримера) не_возникает...
К тому же, если приём обобщается и Шпрага-Гранди с этим приёмом можно использовать для любой игры, где тот, кому некуда ходить, выигрывает -- почему практически во всех источниках рассматривается только случай, когда тот, кому некуда ходить, проигрывает?