Интересный вопрос.
При изоморфизме у нас могут переставиться

Значит, надо смотреть на соотношения между

не зависящие от перестановки. А при перестановке переставляются друг с другом


Варианты:
 - среди элементов есть выделенный
- среди элементов есть выделенный 
 - элементы идемпотенты, выделенного нет.
- элементы идемпотенты, выделенного нет.
 - я не уверен, что есть такое слово, но назовём это "антиидемпотенты". Выделенного нет.
- я не уверен, что есть такое слово, но назовём это "антиидемпотенты". Выделенного нет.

Варианты:
 - один элемент поглощает другой, есть выделенный
- один элемент поглощает другой, есть выделенный 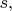 такой что при
такой что при 
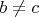 - здесь можно выделить подварианты "левый элемент поглощает правый" и "правый элемент поглощает левый".
- здесь можно выделить подварианты "левый элемент поглощает правый" и "правый элемент поглощает левый".
Итого, получаются такие сочетания:
Итого, 10 классов изоморфизма. В каждой клетке, где есть некий выделенный элемент, он может быть или

или

и класс эквивалентности изоморфизма насчитывает 2 структуры (помечено

). В остальных классах по одной структуре. Всего получается 16 - всё сходится.
-- 07.11.2018 21:29:00 --Расставлю здесь известные мне бинарные функции:
-- 07.11.2018 21:32:13 --Замечание: если позволить вместе с изоморфизмом антиизоморфизм (меняющий местами левые и правые операнды), то вторая и третья строчки сливаются, и получается 7 классов.
-- 07.11.2018 21:38:16 --Хм-м-м...