Хронологический алгоритм для гипотезы Коллатца
Хронологическим алгоритмом для гипотезы Коллатца называется такой алгоритм действий, при
котором для заданного нечётного числа

и числа

сначала выполняется инверсия условий гипотезы
Коллатца начиная с

до числа

, а после выполняются условия гипотезы Коллатца для числа

до достижения последовательности числа 1.
Нечётные числа

не имеют антецедентных нечётных чисел, так как

по инверсии гипотезы Коллатца.
То есть, никакое нечётное число не может спустится до числа вида

(на числа делящиеся на

без остатка).
Пример:

;

;

;

;

и
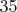
не делятся на три, тем самым

не имеет антецедентных нечётных чисел в гипотезе Коллатца.
Pari/GP code спуска числа

к

:
Код:
{a=23;n=0;while(a>1, if(Mod(a,2)!=0,print1(a*3+1,";"," "); a=(a*3+1)/2; print1(a,";"," "); n++);
while(Mod(a,2)==0,a=a/2;n++; print1(a,";"," "));n++);print("[",a," ",n,"]")}
Pari/GP code инверсии гипотезы Коллатца для числа

и степени двойки

(пример:

) :
Код:
{m=1; a=13; while(Mod(a,3)!=0, if(Mod(a,3)==1, a=(2^(2*m)*a-1)/3,
if(Mod(a,3)==2, a=(2^(2*m-1)*a-1)/3)); print(a))}
Pari/GP code хронологического алгоритма для числа

:
Код:
{m=1;
a=27;
while(Mod(a,3)!=0, if(Mod(a,3)==1, a=(2^(2*m)*a-1)/3,
if(Mod(a,3)==2, a=(2^(2*m-1)*a-1)/3)));
n=0;while(a>1, if(Mod(a,2)==1,print1(a*3+1,";"," ");
a=(a*3+1)/2; print1(a,";"," "); n++);while(Mod(a,2)==0,a=a/2;
n++; print1(a,";"," "));n++);print("[",a," ",n,"]")}