Помогите, пожалуйста, разобраться со следующим вопросом.
Сначала определение: полный предпорядок (полное транзитивное бинарное отношение)

на топологическом пространстве

называется
непрерывным, если для любого
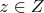
множества

и

замкнуты (можно также доказать, что требование непрерывности эквивалентно тому, что множество

замкнуто в

в топологии прямого произведения).
Пусть

и

- топологические пространства,

- полный предпорядок на

. Пусть имеется непрерывная и сюръективная функция

(где на

задана обычная евклидова (=порядковой) топология), такая, что



.
Я пытаюсь доказать "кажущийся очевидным" факт, что если предпорядок

непрерывен в топологии прямого произведения на

, то и полный предпорядок

на

, построенный по правилу



, также непрерывен в топологии прямого произведения на

.
Мои попытки: я пытался рассматривать фактор-топологию на

, где отношение эквивалентности

определяется как



и

. Однако, не смог доказать, что

гомеоморфно

. Пытался рассматривать фактор-топологию на

, где отношение эквивалентности

определяется как



. Но не смог доказать, что

гомеоморфно

...
Буду благодарен любым комментариям.