... скорее всего, что без факторизации никак.
Да, похоже на то. Это касается и дискретного логарифма. Собственно, и факторизация

не всегда результативна. Поменяем обозначения:

- индекс наименьшего Фибоначчи, кратного

. Такой пример:

Ни на
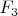
, ни на

не делится, однако же

Вот и квазипростое. Тут надо подумать. Со степенями более-менее понятно, здорово Вы с ними разобрались, спасибо. Самое трудное оказалась пятерка! Страшнее кошки зверя нет:) В
параллельной теме описывается алгоритм вычисления

(там это называется

, надо бы поменять терминологию). Факторизовать

можно попробовать через последовательность

и т.д. Если бы всё-таки захотелось. Оказывается

и

, причем первое зациклено само на себя, ко второму приходит последовательность от любого

, и очень быстро. Просто в качестве наблюдения, об остальном пока рано.