Интегральное представление Зоммерфельда

[zpal]

Известно интегральное представление Зоммерфельда, которое для функций Ханкеля первого рода имеет вид $H_{\nu}(z)=\frac{1}{\pi}\int\limits_{L_2}^{}e^{iz\cos t}e^{i\nu(t-\pi/2)}dt$. Здесь $L_2$ - путь интегрирования на комплексной плоскости, находящийся в пределах от $-\eta+i\infty$ до $\eta-i\infty$, где $0\leqslant\eta\leqslant\pi$, а $-\eta<\arg(z)<\pi-\eta$. Картинку с изображением пути интегрирования не вставляю, поскольку она известна и есть, например, в справочнике Ямке, Эмде и Лёша (с. 222, М. 1968).
Если теперь взять натуральный логарифм от функции нулевого порядка, то получим

$$\ln(H_0(z))=\frac{1}{\pi}\int\limits_{L_2}^{}\ln(e^{iz\cos t})dt=\frac{1}{\pi}\int\limits_{L_2}^{}(iz\cos t+2\pi im)dt=\frac{1}{\pi}iz\int\limits_{L_2}^{}\cos tdt+2im\int\limits_{L_2}^{}dt.$$

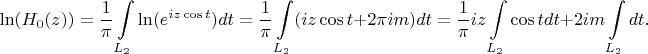
Однако второй интеграл здесь должен быть равен бесконечности. В чем ошибка?
Второй вопрос. Если взять производную от данного логарифма, то получим

$$\frac{d\ln H_0(z)}{dz}=\frac{i}{\pi}\int\limits_{L_2}^{}\cos tdt $$

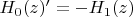
Правая часть не зависит от z. Однако левую часть можно преобразовать как $\frac{d\ln H_0(z)}{dz}=\frac{H_0'(z)}{H_0(z)}=-\frac{H_1(z)}{H_0(z)}$ (здесь учтено, что $H_0(z)'=-H_1(z)$). Получившееся выражение зависит от z, что можно проверить, построив его график в математическом пакете.

[Red_Herring]

zpal в сообщении #1335931 писал(а):

сли теперь взять натуральный логарифм от функции нулевого порядка, то получим

Логарифм от интеграла равен интегралу от логарифма? Срочно премию клиенту

[zpal]

Да, ступил. Можно удалить тему.