Пусть в некотором евклидовом пространстве (вообще трёхмерном, но это не должно успокаивать) есть единичный вектор

, и мы хотим сгенерировать вектор

, распределённый в подпространстве

(а) стандартно нормально или (б) равномерно по его единичной сфере.
Можно ли это сделать и не находя базиса

(я был бы ещё может быть не против, если бы для неизменного

надо было нагенерировать кучу разных

, но он каждый раз будет чуть-чуть другой), и генерируя

нормально распределённых значений?
У меня решается задача (б), а задача (а) здесь добавлена для полноты; текущий способ такой: берётся
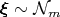
, вычисляются

(выкинули лишнюю размерность),

(выкинули длину). Как видно, этот способ удовлетворяет первому, но не второму требованию, и хотя не жалко сгенерировать лишнюю величину, всё же интересно, нельзя ли что-то сделать.
Почему я тут так против базиса: понятно, что аргумент от инвариантности тут не прокатывает, потому что это непосредственные вычисления, но есть другой: находя базис, мы должны будем сделать произвольный выбор, который потом канет в Лету. Это вызывает желание соптимизировать.