Показать, что если два подпространства
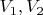
пространства

имеют общим только нулевой вектор
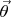
, то сумма их размерностей не превосходит размерности

.
Будем доказывать от противного. Пусть это не так, т.е. подпространства имеют общим только нулевой вектор
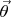
, но сумма их размерностей больше размерности

. Зафиксируем в пространстве

базис

, а в подпространствах
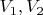
базисы

и

соответственно, при этом имеем, что

. Рассмотрим систему векторов

. Она линейно независима, т.к. подпространства имеют общим только нулевой вектор
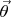
(!). При этом каждый вектор из этой системы является линейной комбинацией базисных векторов

пространства

. Тогда из основной леммы о линейной зависимости следует неравенство
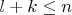
. Получили противоречие с предположением из начала рассуждений, следовательно оно не верно.
Меня интересует момент, который я пометил восклицательным знаком. Достаточно ли корректно такое утверждение? Просто именно на нем основано дальнейшее применение леммы (в ней линейная независимость другой системы является достаточным условием) и получение противоречия.