Как вы перешли от третьей к четвёртой строчке?
разделил на
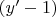
За такое "решение " в контрольной работе школьникам снижают оценки. А как Вас в школе учили решать уравнения типа

?
можем ввести дополнительное условие, при котором
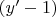
не равен 0
В условии задачи такое ограничение было? Не было. С уравнением при

что-нибудь плохое происходит? Не происходит. Значит, не вводим.
была идея с комплексными числами решить
Если бы комплексные числа имелись в виду, об этом было бы явно сказано. Раз комплексные числа не упоминались, значит вводить их не надо.