Упражнение из учебника Гельфанда по линейной алгебре

[ioleg19029700]

Доказать, что если $V_1$ и $V_2$ - подпространства пространства $V$ такие, что $V_1 \subset V_2$ и $\dim V_1 = \dim V_2=k$, то $V_1=V_2$. То есть нужно показать, что любой вектор из $V_2$ является линейной комбинацией базисных векторов $V_1$?
Тогда зафиксируем в $V_1$ базис $\vec{e_1},\ldots, \vec{e_k}$. Т.к. $V_1 \subset V_2$ и их размерности совпадают, то $\vec{e_1},\ldots, \vec{e_k}$ - базис в $V_2$. Таким образом $v = a_1\vec{e_1} + \ldots + a_k\vec{e_k}$ $,\forall v\in V_2$. Ч.т.д.
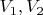
Это достаточно аккуратно? Как-то настолько просто, что вот даже сюда пишу. Я вот нигде (ведь так?) не использовал факт того, что $V_1, V_2$ - это подпространства пространства $V$, и это не дает мне покоя. Нет ли в доказательстве какого-то некорректного перехода?

[mihaild]

Необходимые свойства базисов к этому моменту уже известны? В частности, что любая линейно независимая комбинация нужного размера является базисом?
Если да - то всё честно.

ioleg19029700 в сообщении #1333218 писал(а):

Я вот нигде (ведь так?) не использовал факт того, что $V_1, V_2$ - это подпространства пространства $V$,

Это используется в формулировке - чтобы говорить про размерности, линейные комбинации и т.д.

[ioleg19029700]

mihaild
Да, данный факт про базис известен. Спасибо