Цитата:
Рассмотрим матрицу размера
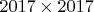
, содержащую числа

. Числа в ней записаны в порядке начиная с левого верхнего угла, двигаясь по строкам слева направо и сверху вниз, т.е. первое число, записанное во второй строке, равно

. В этой матрице выбрано 2017 чисел так, что в каждой строке и каждом столбце выбрано ровно одно число.
Найдите максимальное значение, которое может принимать сумма этих чисел.
Скорее всего, тут есть какой-то хитрый подход, но я пошел прямолинейным путем — рассмотрел сначала матрицу

, затем

. Интуитивно кажется, что все просто, и сумма элементов, стоящих на главной диагонали матрицы, как раз и будет максимальной. То есть максимальная сумма для квадратной матрицы размера

равна

.
Можно ведь здесь применить индукцию? И вообще, может, как-то иначе нужно рассуждать.