Я пишу про параметры, получаемые методом step regression в результате симуляций, строго говоря, оценками среди них можно назвать только

, потому что только они оцениваются, и только они уменьшают число степеней свободы дисперсии остатков, на основании которой и рассчитывается доверительный интервал.

- это строго говоря не оценки, они задаются априори, перед оцениванием неизвестных параметров. Но всё это есть отклонение от темы и не суть важно.
Цитата:
... ведь если мы делаем ступенчатую регрессию с AIC штрафом, то она выкидывает все переменные которые не прошли 0,157 барьер по p-value
AIC не статистика, к нему вообще не применимы такие понятия как p-value
если выбрасываются все переменные, которые не прошли 0,157 барьер по p-value, то это не step regression, а похоже на простой отбор по t критерию. Какую роль здесь играет AIC если отбор осуществляется по t критерию? Мне это не понятно.
Цитата:
Я исходил из идеи идеальной модели. Что такое идеальная модель? Это модель, которая дает 95% покрытие для всех хоть сколько-то значимых параметров и 100% выкидывает все ненужные (

).
Идеальная модель, это модель, в которой cover совпадёт с

доверительного интервала, вот и всё. Если у Вашего доверительного интервала

, то да, все истинные значения параметров должны покрываться в 95% случаев. Причём и

тоже в 95% случаев, а не как вы пишите 100%. Ноль это такое же значение, как и все остальные.
Цитата:
если я использую метод усреднения моделей, так что в каждой итерации у меня есть и оценка для

и доверительный интервал, то высчитав процент покрытия я могу сказать годен (valid) ли он, просто проверив если он в пределах
![$[93.6,96.4]$ $[93.6,96.4]$](https://dxdy-04.korotkov.co.uk/f/3/d/9/3d949bbbaea8887ffe451ebc96516c4a82.png)
. А если, при этом, я основываю свой анализ ступенчатой регрессии на 50 итерациях, то теперь этот предел
![$[75.8, 100]$ $[75.8, 100]$](https://dxdy-02.korotkov.co.uk/f/d/7/2/d72c94f1e1235da9b3125140bfbdfb6082.png)
. В таком случае, как я могу сравнить эти два метода - метод усреднения моделей и ступенчатой регрессии?
Если это так, то сравниваемые методы дают вам разные доверительные интервалы. Есть такое понятие как эффективность оценок. В зависимости от данных, разные методы обеспечивают разную эффективность. В Вашем случае, первый метод более эффективен, так как доверительный интервал уже. Доверительный интервал, если он адекватен, не должен зависеть от числа итераций.
Цитата:
В статье, они поменяли количество итераций, увеличив из в 10 раз для ступенчатой регрессии, но я не могу так сделать.
Видимо это сделано не просто так. Если Вы этого не можете, то лучше ограничится небольшим числом итераций, чем подгонять результаты под свои ожидания. Ведь именно к этому Вы и стремитесь.
Цитата:
я заранее знаю, что методы ступенчатой регрессии, лассо и иже с ними отсеются на первой же стадии
,
это лишь Ваше личное предположение. На самом деле, если эти методы применяются корректно, то обеспечивают результаты близкие к теоретическому пределу. Это давно доказано. А у Вас нормально распределённые остатки. Тут сомнительно обнаружить какие то недостатки.
К стати, как Вы оцениваете доверительные интервалы для LASSO?
Цитата:
Опять же, меня не сильно волнует длина интервала. Я сравниваю несколько методов, и начинаю сравнение с процента покрытия, если метод показал плохой процент, я его бракую.
Это правильно, если cover не совпадает с

, то доверительные интервалы неадекватны и нет никакого смысла ориентироваться на их величину.
Но нужно иметь в виду, если

это тоже плохо. Например, если cover=98%, а
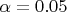
, то ничего хорошего в этом нет. Это означает, что теоретические оценки доверительных интервалов шире реальных, и метод на самом деле более эффективен, чем это кажется. В этом случае, разумеется, отбраковывать метод не стоит, но и доверительные интервалы не годятся для того, чтобы по ним оценивать качество метода. Нужно оценивать адекватные доверительные интервалы, каким то другим способом.