Потому что множество равномощно некоторому кардиналу тогда и только тогда, когда его можно вполне упорядочить.
У вас проблема с формулировкой "ответить на вопрос" (тогда см. строчкой выше формальное утверждение) или с доказательством формального утверждения? Если второе - напишите, какие у вас есть идеи, как его доказать, и где затык. Подсказка: чтобы доказать эквивалентность, в данном случае нужно доказать два следствия (слева направо и справа налево).
Второе, в одну сторону: если множество вполне упорядочено, то оно изоморфно, а значит и равномощно, некоторому ординалу, но нужна равномощность не просто ординалу, а кардиналу, как показать, что и такой будет?
В другую: если множества

равномощны, то существует биекция
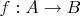
, тогда если на множестве

есть порядок, то определим порядок на

таким образом:
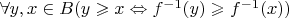
. Тогда и вполне упорядоченность сохранится.