Хи-квадрат критерий согласия. Вопросы.

[_hum_]

Евгений Машеров в сообщении #1332343 писал(а):

Группировку при расчёте параметров распределения ныне не используют. Это загрубление, использовавшееся для сокращения объёма ручного счёта (вручную посчитать число попаданий в ячейку проще, чем умножать).

Нет. Без группировки у вас получатся оценки, которые при подстановке в статистику приведут к зависимости ее предельного распределения от параметров, см. Chernoff and Lehmann. The Use of Maximum Likelihood Estimates in χ2 Tests for Goodness of Fit (1954).

Евгений Машеров в сообщении #1332343 писал(а):

G-тест способен работать при малом числе наблюдений в ячейке в силу того, что при малом числе величина под логарифмом не настолько близка к единице, чтобы пренебречь членами ряда для логарифма степени выше второй. А это пренебрежение даёт нам совпадение с формулой для критерия $\chi^2$

Ваши рассуждения строятся на условии совпадения статистик. Но кто сказал, что это необходимо?

Александрович, спасибо. Только там все-таки больше рекомендации, а хотелось бы еще и понимать, почему так, а не иначе.

[Евгений Машеров]

Строго говоря, Вы правы. Совпадают распределения только асимптотически. Однако с практической точки зрения и по результатам моделирования разницы нет. Осторожные заявления "лежит между $\chi^2_{k-1}$ и $\chi^2_{k-s-1}$" - сильная перестраховка.

[_hum_]

Евгений Машеров в сообщении #1332412 писал(а):

Совпадают распределения только асимптотически.

Мм.. Если только вы имеете в виду асимптотичность при стремлении числа карманов к бесконечности. В противном случае (при стремлении объема выборки к бесконечности) совпадения не будет.

Евгений Машеров в сообщении #1332412 писал(а):

Однако с практической точки зрения и по результатам моделирования разницы нет.

Опять же, это наверное потому, что те случаи, о которых вы ведете речь, либо с малым количеством параметров, либо с большим количеством карманов.

Кстати, в той статье, ссылку на которую вы давали, был фраза:

Цитата:

Максимальную мощность критерии c^2 Пирсона и отношения правдопо­добия зачастую имеют или при минимально возможном числе интервалов, определяемом условием r= k-m-1 ³1 , или при оптимальном числе интервалов, близком к минимально возможному.

по которой вроде бы следует, что число карманов должно быть примерно сравнимым с числом оцениваемых параметров. С учетом этого, пренебрежение разницей возможно только при большом числе параметров.

И, господа знатоки, как использовать все-таки использовать "Таблицы асимптотически оптимального группирования при проверке гипотез о согласии с использованием критериев типа c^2 Пирсона и оценивании параметров" - каким образом по ним выбирать схему построения карманов? (Это хоть как-то бы улучшило ситуацию с моей проблемой выбора карманов для Хи-квадрат).

[_hum_]

Кстати, а почему нельзя тестирование сложной (параметрической) гипотезы свести к тестированию простой по схеме:
1. Для всех возможных параметров $\theta$ сложной гипотезы
1.1 выполнить тестирование простой гипотезы $H_0 = (P=P_\theta)$, найдя $p$-value;
2. Вывести в качестве результата максимальное из найденных $p$-value.
?

[GAA]

_hum_ в сообщении #1332206 писал(а):

1) изначально (вне зависимости от выборки) задается $k$-карманов;

В случае сложной гипотезы мы не можем задать разбиение (по-другому, задать промежутки группировки, классы, разряды,…) до получения данных.
Ещё задолго до 70-х годов было замечено, что для распределений с ограниченным носителем при оценке определяющих носитель параметров методом максимального правдоподобия число степеней свободы не уменьшается на число оцениваемых параметров. [Некоторые сведения касающиеся этого изложены в книге Кендалл и Стьюарт «Статистические выводы и связи», 1973] Для «регулярных» распределений (к числу которых относится нормальное) при практических расчетах поступали следующим образом. Сначала по исходной выборке находили оценки параметров, затем на основе этих оценок строили интервалы, в частности, с «равной ожидаемой вероятностью классов» (обозначим число интервалов группировки через $k$), затем находили оценки параметров методом минимума $\chi^2$ или им асимптотически эквивалентные, и на основании этих оценок вычисляли значение статистики. Считалось, что с ростом объёма выборки распределение статистики стремится к распределению $\chi^2$ с числом степеней свободы $k-s-1$, где $s$ — число оцениваемых параметров. В начале 70-х годов была доказана справедливость этого метода для точно сформулированных классов распределений. См. Чибисов Д. М. Некоторые критерии типа хи-квадрат для непрерывных распределений// Теория вероятн. и ее примен., 1971, т. 16, вып. 1, с. 3–20

_hum_ в сообщении #1332206 писал(а):

2, вариант B) находится оценка максимального правдоподобия параметра $\Tilde{\theta}$ по несгруппированной выборке;

В этом направлении разрабатывались модификации критерия $\chi^2$, начиная с работы K. C. Rao and D. S. Robson, “A chi-square statistics for goodness-of-fit tests within the exponential family,” Commun. Statist., 3, 1139–1153 (1974). Можно нагуглить эту статью и продолжение этой линии. Upd. Можно ещё посмотреть диссертацию на мастера Hutchinson D. “Modern developments in chi-square goodness-of-fit testing.” (1977).

_hum_ в сообщении #1332206 писал(а):

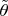
4, вариант B) если используется $\tilde{\theta}$, то полагаются на результат, что в этом случае распределение будет зависеть от параметра, но при этом находиться (функция распределения будет принимать значения) между хи-квадрат с $k$ - число оцененных параметров - 1 и хи-квадрат с $k$- 1, а потому можно смело отвергать гипотезу на выбранном уровне значимости, если значение критерия выше (соответствующего уровню значимости) квантиля для хи-квадрат с $k$ - 1, и смело не отвергать, если оно меньше квантиля для хи-квадрат с $k$ - число оцененных параметров - 1, с оставшейся серой зоной между этими двумя квантилями (когда ничего нельзя сказать).

Опечатки, но мысль понятна.

_hum_ в сообщении #1332206 писал(а):

Все прекрасно, кроме того, как в этом случае выбирать число карманов и их ширину?

Выбор числа интервалов зависит от рассматриваемых альтернатив. См. в Kендалл и Стьюарт пп. 30.28–30.29 и ссылки там. Выбор интервалов с равными вероятностями классов, очевидно, плодотворен при большом числе интервалов группировки. При большом числе интервалов (классов) при таком выборе уменьшается число случаев, когда статистика критерия не может быть вычислена. Более того, по моему опыту, итерационные процедуры при таком выборе интервалов в случае нормально распределения сходятся (может быть (не проверял) кроме экзотически малых объёмов выборок, но я не сталкивался).

_hum_ в сообщении #1332206 писал(а):

Не совсем понял, как использовать "Таблицы асимптотически оптимального группирования при проверке гипотез о согласии с использованием критериев типа c^2 Пирсона и оценивании параметров" - каким образом по ним выбирать схему построения карманов?

По ссылке (в теме выше) приведены примеры; посмотрите оглавление. Лучше задать более конкретный вопрос.