Мне попался листочек с задачами одной из матшкол.
Там была одна задача, которую у меня не получилось решить, причем задача кажется довольно интересной.
Утверждается, что она для 8 класса и стояла первой в списке задач, но я потратил часа 3 в сумме на нее, и получились лишь некоторые весьма ограниченные продвижения.
Задача. Пусть
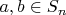
- циклы,

. (Циклы в обычном смысле,

) Доказать, что

тогда и только тогда, когда выполняется одно из двух условий:
1) Циклы независимы (то есть
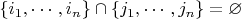
).
2)

и

. НОД обозначен как

.
У меня получилось доказать достаточность.
А именно - пусть выполнено первое условие. Тогда, очевидно, при перемножении они друг на друга не влияют и получается, что ответ не зависит от порядка умножения.
Если же выполнено второе условие, то

С необходимостью же уже все гораздо сложнее.
Можно считать, что перестановки пересекаются. Если бы это было не так, выполнялось бы первое условие и на этом можно было бы закончить.
То есть нам нужно доказать, что если

и

, то

для некоторого

.
(Еще не забыть про то что длины должны быть равны и что длина взаимно проста с

)
Дальше уже ступор. Мне сейчас кажется продвижением думать про подгруппу в

, порождаемую всеми возможными комбинациями

и

. Если бы

и

не коммутировали бы, то в этой группе были бы элементы вида

и подобные, но у нас по условию

и поэтому произвольный элемент подгруппы выглядит как

для некоторых

. Все аксиомы группы выполняются, более того, есть коммутативность.
Потом идея рассматривать элементы

. Если здесь окажется единичная перестановка, мы почти победили (нужно еще установить, что если такое

нашлось, то по нему надо построить взаимно простое с длиной
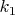
и что вообще длины совпадают).
Подгруппа конечной группы конечна. У любого элемента есть конечный порядок.
Посмотрим на порядок элемента

. Найдем
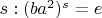
и

.

Теперь найдем такие

что
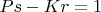
. Такие

найдутся, если
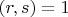
.
Тогда

Тут еще надо думать про

и

.
Тут я увяз. Что можно сказать про взаимную простоту

и

? Не использовал, что

, так что, возможно, вообще не в ту степь иду.
Решений для листочков нет, поэтому прошу помочь :(