Подскажите пожалуйста специальную функцию, для которой преобразование Лапласа имеет вид
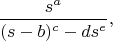
где

, то есть могут быть нецелыми положительными.
В справочнике Бейтмен Эрдейи Таблица интегральных преобразований 1969. Том 1. не нашел.
Буду благодарен за ссылку на книгу справочник или статью (рус или анг),
в которой есть о ней какая-нибудь информация.
Заранее спасибо.