Немножко по поводу возможной мотивации аксиом теории вероятностей.
Можно рассматривать вероятность как математическую модель относительной частоты события. Поэтому свойства вероятности должны быть такими же, как свойства относительной частоты.
Относительной частотой события

в

опытах называется отношение числа появлений

события

к числу проведённых опытов, то есть,

.
Относительная частота обладает следующими очевидными свойствами:
1)

;
2)

, где

- достоверное событие;
3) если события

и

несовместны, то

;
3') если события

попарно несовместны, то

.
Последнее свойство есть

-аддитивность относительной частоты, и оно является тривиальным следствием предыдущего свойства (аддитивности), поскольку в

опытах может произойти не более

попарно несовместных событий, то есть, только конечное число. Поэтому сумма в правой части, на самом деле, содержит не более

ненулевых слагаемых.
Можно пойти немного дальше. Предположим, что опыты у нас ставятся не как попало, а все в одинаковых условиях, так что шансы появления события в каждом опыте одни и та же и никак не зависят от результатов других опытов в этой серии.
В таких предположениях событие называется
статистически устойчивым, если его относительная частота имеет предел при

. Этот предел называется
вероятностью события:

При таком подходе кажется само собой разумеющимся, что вероятность должна обладать такими же свойствами, что и относительная частота.
Однако это определение - плохое. Ясно, что "предел" в этм определении имеет весьма отдалённое отношение к пределу последовательности, изучаемому в курсе математического анализа. Поскольку члены последовательности в данном случае определяются с помощью вовсе не математической процедуры (случайных испытаний), то никаких предположений о поведении этой процедуры мы делать не можем. Если мы бросаем симметричную монету, интересуясь вероятностью выпадения одной из ей сторон, то нет никаких гарантий того, что в пределе получится
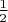
, или вообще что-нибудь получится. Никто не может запретить этой монете всегда падать одной и той же стороной - при всей её симметрии. Поэтому "предел" этот нуждается в специальном определении. Смысл этого предела описывается усиленным законом больших чисел для схемы Бернулли, и его формулировка в действительности требует, чтобы понятие вероятности уже было определено. Может быть, эту проблему и можно как-нибудь обойти, но я в эти вопросы никогда не вникал.