Принцип Даламбера-Лагранжа, формальный аспект

[pogulyat_vyshel]

ПРИНЦИП ДАЛАМБЕРА-ЛАГРАНЖА

Рассмотрим систему материальных точек с массами $m_1,\ldots,m_N$ и радиус-векторами $\boldsymbol r_1,\ldots \boldsymbol r_N$. Многообразие $\Sigma=\{(\boldsymbol r_1,\ldots \boldsymbol r_N)\in\mathbb{R}^{3N}\}$ назовем конфигурационным многообразием системы.
Будем считать, что во все время движения радиус-векторы удовлетворяют следующим уравнениям:

$$ \sum_{k=1}^N(\boldsymbol a_{kj},\boldsymbol{\dot r}_k)+b_j=0,\quad j=1,\ldots,n<3N,\qquad (1)$$

где $\boldsymbol a_{kj},b_j$ являются функциями от $t,\boldsymbol r_1,\ldots, \boldsymbol r_N$. Уравнения (1) называются связями.
Будем считать, что векторы $\xi_j=(\boldsymbol a_{1j},\ldots,\boldsymbol a_{Nj})\in\mathbb{R}^{3N}$ линейно независимы при всех $t,\boldsymbol r_1,\ldots, \boldsymbol r_N$.
ОПРЕДЕЛЕНИЕ 1. Пространством виртуальных перемещений называется множество векторов $(\delta\boldsymbol r_1,\ldots \delta\boldsymbol r_N)\in \mathbb{R}^{3N}$, удовлетворяющих системе уравнений

$$\sum_{k=1}^N(\boldsymbol a_{kj},\delta\boldsymbol{ r}_k)=0,\quad j=1,\ldots,n.\qquad (2)$$

Удобно рассматривать множество виртуальных перемещений как подпространство касательного пространства к многообразию $\Sigma$ в точке $(\boldsymbol r_1,\ldots, \boldsymbol r_N)$ при заданном $t$.
Размерность пространства виртуальных перемещений (она равна 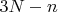$3N-n$) называется числом степеней свободы системы.
Множество векторов $(\boldsymbol {\dot r}_1,\ldots \boldsymbol{\dot r}_N)$, удовлетворяющих (1), называется множеством действительных перемещений. (Это определение отличается от стандартного: обычно действительными перемещениями называются дифференциалы $d\boldsymbol r_k=\boldsymbol{\dot r}_kdt,$.)
Во многих задачах связи не зависят явно от скоростей и задаются уравнениями вида

$$f_j(t,\boldsymbol r_1,\ldots, \boldsymbol r_N)=0.$$

Такие связи называются геометрическими. Дифференцируя эти уравнения по времени, мы получим уравнения вида (1):

$$ \frac{\partial f_j}{\partial t}+\sum_{k=1}^N\Big(\frac{\partial f_j}{\partial \boldsymbol r_k},\boldsymbol{\dot r}_k\Big)=0.\qquad (3)$$

ОПРЕДЕЛЕНИЕ 2. Если существует набор функций $f_1,\ldots,f_n$ такой, что при всех $t,\boldsymbol r_1,\ldots, \boldsymbol r_N$ множество действительных перемещений, заданное уравнениями (1), совпадает с множеством действительных перемещений, заданным уравнениями (3), то связи (1) называются голономными, в противном случае связи (1) неголономны.


ОПРЕДЕЛЕНИЕ 3. Силы, вынуждающие точки $m_1,\ldots m_N$ двигаться в соответствие с уравнениями (1), называются реакциями связей. На каждую точку $m_k$ действует реакция связи $\boldsymbol R_k.$
Связи (1) называются идеальными, если для любого набора виртуальных перемещений выполнено равенство

$$ \sum_{k=1}^N(\boldsymbol R_k,\delta\boldsymbol r_k)=0.\qquad (4)$$

Дальше рассматриваются только идеальные связи.
Предположим, что сумма всех сил, действующих на точку $m_k$ равна $\boldsymbol G_k$.

ОПРЕДЕЛЕНИЕ 4. Силы $\boldsymbol F_k=\boldsymbol G_k-\boldsymbol R_k$ называются активными силами.

Уравнения движения системы материальных точек приобретают вид

$$m_k\boldsymbol{\ddot r}_k=\boldsymbol F_k+\boldsymbol R_k,\quad k=1,\ldots, N.\qquad (5)$$

Следующая теорема является прямым следствием формул (4),(5).

ТЕОРЕМА 1. Пусть $\boldsymbol r_1(t),\ldots,\boldsymbol r_N(t)$ -- закон движения системы. Тогда для любого набора виртуальных перемещений выполнено равенство

$$ \sum_{k=1}^N(m_k\boldsymbol{\ddot r}_k-\boldsymbol F_k,\delta \boldsymbol r_k)=0.\qquad (6)$$

ТЕОРЕМА 2. Предположим, что при некоторых $t_0,\boldsymbol {\hat r}_1,\ldots \boldsymbol {\hat r}_N$ задан набор действительных перемещений $\boldsymbol v_1,\ldots \boldsymbol v_N$.
Тогда существует, и притом единственный, набор функций $\boldsymbol r_1(t),\ldots,\boldsymbol r_N(t)$ такой, что
1) $\boldsymbol r_k(t_0)=\boldsymbol {\hat r}_k,\quad \boldsymbol{\dot r}_k(t_0)=\boldsymbol v_k;$
2) функции $\boldsymbol r_1(t),\ldots,\boldsymbol r_N(t)$ удовлетворяют уравнению (6) для любого набора виртуальных перемещений;
3) функции $\boldsymbol r_1(t),\ldots,\boldsymbol r_N(t)$ удовлетворяют системе (1).

Доказательство теоремы 2. Предположим сперва, что указанный в теореме набор функций существует. Докажем единственность.

ЛЕММА 1. Пусть $X$ -- векторное пространство и $u,u_1,\ldots,u_l:X\to\mathbb R$ -- линейные функционалы.

Если

$$\bigcap_{k=1}^l\mathrm{ker}\, u_k\subseteq \mathrm{ker}\, u$$

тогда существует набор чисел $\lambda_1,\ldots,\lambda_l$ такой, что

$$u=\sum_{k=1}^l\lambda_k u_k.$$

По этой лемме и из формул (6), (2) получаем

$$m_k\boldsymbol{\ddot r}_k=\boldsymbol F_k+\sum_{j=1}^n\lambda_j\boldsymbol a_{kj}.\qquad (7)$$

Покажем, что $\lambda_j$ определены однозначно и зависят от $t,\boldsymbol{ r}_k,\boldsymbol{\dot r}_k,\quad k=1,\ldots,N.$

Продифференцируем формулу (1) по времени:

$$\sum_{k=1}^N(\boldsymbol a_{kj},\boldsymbol{\ddot r}_k)+w_{j1}=0,$$

где $w_{j1}$ -- функция от $t,\boldsymbol{ r}_k,\boldsymbol{\dot r}_k,\quad k=1,\ldots,N.$

Подставим в эту формулу ускорения из (7), получим

$$ \sum_{k=1}^N\sum_{s=1}^n\frac{1}{m_k}(\boldsymbol a_{kj},\boldsymbol a_{ks})\lambda_s+w_{j2}=0,\qquad (8)$$

где $w_{j2}$ -- функция от $t,\boldsymbol{ r}_k,\boldsymbol{\dot r}_k,\quad k=1,\ldots,N.$
Матрица $A_{js}=\sum_{k=1}^N\frac{1}{m_k}(\boldsymbol a_{kj},\boldsymbol a_{ks})$ системы линейных алгебраических уравнений (8) невырождена. Действительно, эта
матрица является матрицей Грамма векторов $\xi_i$ при следующем скалярном произведении в $\mathbb{R}^{3N}$

$$\langle \xi_j,\xi_s\rangle =\sum_{k=1}^N\frac{1}{m_k}(\boldsymbol a_{kj},\boldsymbol a_{ks}).$$

Таким образом, функции $\lambda_j$ находятся из (8) однозначно.
Теперь единственность вытекает из теоремы существования и единственности Коши для системы (7). Отсюда же вытекает и существование, поскольку.
по построению, функции

$$\phi_j=\sum_{k=1}^N(\boldsymbol a_{kj},\boldsymbol{\dot r}_k)+b_j$$

являются первыми интегралами системы (7).

Система уравнений (7) называется системой уравнений Лагранжа первого рода.

[pogulyat_vyshel]

ну вот собственно вот :) Все уравнения аналитической механики (уравнения Лагранжа, различные формы уравнений неголономной механики, вариационные принципы, общие теоремы динамики со связями) следуют из теорем 1, 2