Не могли бы вы проверить, правильно ли я использую принцип (метод) математической индукции при доказательстве теоремы? Вот его определение:
Пусть

- такое множество, что:
1)

2)

из того, что

. Тогда

. В частности, если

, то

.
Применяя метод мат. индукции, нужно доказать, что для

,
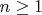
.
Пусть

- множество таких чисел

, что

.
Проверяем

:

- неравенство выполняется, т.е. мы доказали, что

.
Пусть

, т.е. для любого натурального

выполнено

(
тут я на самом деле не знаю как правильно говорить, вряд ли я могу сказать "Пусть для любого натурального

выполнено

")
Проверяем принадлежность

:

(предположение индукции)

(свойства неравенств; выполняется потому что выполнено предыдущее)
Теперь подробнее:

.
Т.е.

удовлетворяет неравенству, т.е.

.
Отсюда

и, поскольку

(не знаю, правда, почему; по-видимому, я должен здесь это сказать), то

и неравенство выполняется для всех натуральных чисел.
Полностью правильно или есть недочёты/ошибки?
Ещё вопрос. Пусть мат. индукцией пытаемся доказать, что

составное число при

. Тут мы не должны доказывать, что

(и не можем этого сделать). Правильно ли я понимаю, что в этом случае речь идёт не о всём множестве

, а о его (неограниченном сверху) подмножестве, имеющем по определению первый элемент, и тогда мы базу индукции доказываем для этого первого элемента (вернее, мы
имеем право это делать, несмотря на то как у меня записан принцип мат. индукции), т.е. для

, и доказываем включение множества

не во всё множество натуральных чисел, а в упомянутое мною подмножество?