Я неудачно выразился - "останавливающаяся МТ" в данном случае значит "МТ, останавливающаяся на пустом входе". Довольно легко сделать детерменированную МТ, которая останавливается на номерах МТ, останавливающихся на пустом входе, и не останавливающуюся на остальных.
Пустой вход -- имеется в виду пустой язык
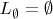
или пустое слово

? В случае пустого языка проблема остаётся такой же, ведь машине нужно будет проверить, что каждое слово

отклоняется машиной, номер которой подаётся ей на вход, и допустить свой вход эта проверяющая МТ не сможет, даже если он является номером какой-то МТ, останавливающейся на пустом входе. В случае пустого слова у ДМТ также могут возникнуть трудности, это произойдёт если поданный ей на вход номер окажется номером НМТ с бесконечными вычислениями, тогда ДМТ при моделировании работы НМТ на пустом слове может пойти по бесконечной ветви дерева вычислений НМТ. Но вот НМТ, она же вроде прекращает вычисления при достижении допускающего состояния, и при моделировании работы другой НМТ на пустом слове (которая останавливается на пустом слове, т.е. имеет конечное допускающее вычисление, но некоторые вычисления на пустом слове при этом могут быть бесконечными), даже если у этой НМТ (вычисления которой моделируются) есть бесконечные ветви, моделирующая НМТ, одновременно исследуя все ветви вычислений той машины, дойдёт до её допускающей конфигурации и прервёт свои вычисления, приняв вход (при условии что НМТ, номер которой подан на вход, останавливается на пустом слове). Странно получается...
Там должны быть какие-то ограничения. Например, требование, чтобы у недетерменированной МТ на всех словах, которые она принимает, существовал принимающий путь вычислимой длины. Или чтобы не существовало бесконечного пути. Или еще что-то равносильное.
Так вроде то, что НМТ допускает какой-то вход, как раз и эквивалентно тому, что у неё есть допускающее вычисление на этом входе, в которое она приходит спустя конечное число шагов (что эквивалентно существованию в её дереве вычислений пути от корня до листа, помеченного допускающей конфигурацией)? Или я что-то путаю...
Т.е., и детерминированная машина никому и ничего не должна, что бы себе ни представлял её создатель. Просто в случае детерминированной легче себе представить вычисляющую модель.
Хотел сказать вот ещё что по этому поводу. Мы же не можем просто говорить "Пусть

-- НМТ, решающая проблему выполнимости булевых формул...", по-хорошему мы должны предъявить алгоритм, следуя которому (являясь которым) машина

будет а) всегда выдавать правильное решение; б) делать это в течение конечного числа шагов. Поэтому, на мой взгляд, естественно задаваться вопросом, как именно должен работать этот недетерминированный алгоритм. А двухэтапная процедура с угадыванием доказательства

и последующей проверкой корректности этого доказательства -- по видимому, самый простой и очевидный способ построения недетерминированных алгоритмов для переборных задач вроде проверки выполнимости булевых формул. По моим представлениям, другие недетерминированные алгоритмы, во-первых, потребуют применения более сложных алгоритмических идей, а во-вторых, не дадут ничего нового для иллюстрации "вычислительной мощи" НМТ по сравнению с ДМТ. Видимо, именно поэтому во многих изложениях при пояснении работы НМТ говорят о ней как о машине, которая при решении задач сначала делает недетерминированное предположение, а затем детерминированно проверяет правильность этого предположения.
Цитата:
Ссылочку можно? Для автоматов с магазинной памятью это не так, точно помню, а реализовать такой автомат на МТ, как понимаю, можно.
Например, уже упомянутая мной выше книга Ю. Громковича (глава про машины Тьюринга). Правда, там говорится о равенстве классов распознаваемых языков для НМТ и ДМТ
без бесконечных вычислений.