Нечётное количество инволюций

[beroal]

Цитата:

Задача 2.8. (i) Пусть $G$ есть конечная группа и $o(G)$ чётно. Верно ли, что количество элементов порядка $2$ в $G$ нечётно — содержит ли любая группа чётного порядка инволюцию? Смотри также теорему Коши (Теорема 6.2).

Согласно определению 2.19.iii, инволюция есть элемент с порядком $2$.

Мои мысли по поводу. Для начала определение: $g\in G$ есть общепринятая инволюция $\iff$ $g\cdot g=1$. $g$ есть общепринятая инволюция $\iff$ порядок $g$ равен $1$ или $2$ $\iff$ $g=g^{-1}$. $o(g)=1 \iff g=1$. Следовательно, количество инволюций нечётно $\iff$ количество общепринятых инволюций чётно.

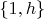
Если $G$ коммутативна, то произведение общепринятых инволюций есть общепринятая инволюция, так как нахождение обратного элемента есть гомоморфизм и $(g\cdot h)^{-1} = g^{-1}\cdot h^{-1} = g\cdot h$. Следовательно, множество всех общепринятых инволюций есть подгруппа группы $G$, обозначим её $H$. Если $H$ содержит ненейтральный элемент $h$, тогда $\{1, h\}$ есть подгруппа группы $H$ и кардинальность $H$ чётна по теореме Лагранжа.

Обозначим количество общепринятых инволюций в $S_n$ как $a_n$. $a_0=1$, $a_1=1$, $a_n=a_{n-1} + (n-1)\cdot a_{n-2}$. Следовательно, $a_2=2$, $a_3=4$ и для всех $n\geq 2$ имеем $2\mid a_n$.

Дальше не знаю, что делать. Ещё меня смущает, что эта задача в начале учебника, до неё только теорема Лагранжа. Подразумевается, что я не должен использовать сложные инструменты.

[vpb]

beroal
1) cardinality по русски "мощность". Применительно к конечным множествам чаще употребляют слово "порядок". А когда речь идет о конечных группах, то слово "порядок" используется практически всегда.
2) Действительно, задача совершенно элементарная, и теорема Лагранжа тут тоже не нужна. Каждому элементу сопоставим его обратный. Т.е. рассмотрим на группе отображение по правилу $g\mapsto g^{-1}$. Это отображение, заметим, инволютивно. ... Понятен ли намек ?

[beroal]

vpb в сообщении #1321334 писал(а):

2) Действительно, задача совершенно элементарная, и теорема Лагранжа тут тоже не нужна. Каждому элементу сопоставим его обратный. Т.е. рассмотрим на группе отображение по правилу $g\mapsto g^{-1}$. Это отображение, заметим, инволютивно. ... Понятен ли намек ?

Мощность множества всех элементов, кроме общепринятых инволюций, чётна. Тогда понятно, спасибо.

vpb в сообщении #1321334 писал(а):

1) cardinality по русски "мощность".

Я знаю, но от чтения английского текста появляются кальки.