Теорема гласит:
"Если у любых

юношей

имеется не меннее

знакомых девушек, то их можно так поженить, что каждому юноше достанется по знакомой девушке."
Тут доказательство:
https://www.mccme.ru/s43/math/uroki/2009_2010/9mat_0910/spec/59_hall_lect.pdfКак-то сложно мне кажется.
Разве нельзя так, например:
Рассмотрим случай, когда у

юношей ровно

знакомых девушки.
Покажем как сопоставить каждому юноше по знакомой девушке.
Выберем произвольного первого юношу. По условию ( для
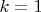
) у него есть одна знакомая девушка. Получается пара которую можно поженить.
Теперь возьмем второго юношу. Теперь (
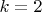
). У них вместе с первым ровно

занкомых дувушки. Если даже у второго юноше среди знакомых девушка первого - то остается еще одна. То есть двоих тоже можно поженить. И так рассуждение можно продолжить далее до

.
В случае если у

юношей более чем

знакомых девушки, то это только добавляет возможностей сосатвить пары.
Что не так в таком доказательстве?